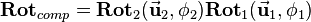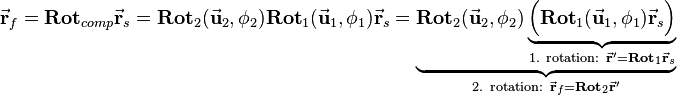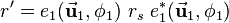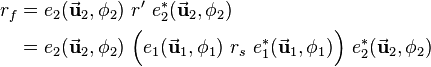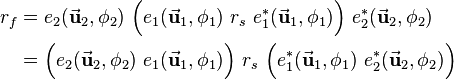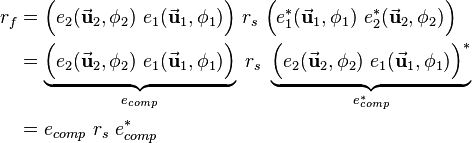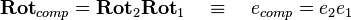Composition of rotations
| ← Back: Rotations using quaternions | Overview: Quaternions | Next: Realization of transformations → |
Usually rotations are regarded around the three coordinate axes  ,
, 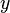 and
and 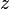 and formulas are known to define the corresponding principal rotation matrices
and formulas are known to define the corresponding principal rotation matrices 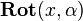 ,
, 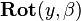 and
and 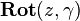 .
.
As explained in the previous article Rotations using quaternions, a rotation around an axis defined by a unit vector 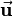 about the angle
about the angle 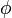 can be described by a quaternion
can be described by a quaternion  as follows:
as follows:
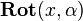 describes a rotation around the
describes a rotation around the 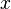 -axis by the angle
-axis by the angle 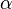 . The
. The 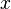 -axis is defined by the unit vector
-axis is defined by the unit vector ![[1\ 0\ 0]^T](/wiki/robotics/images/math/a/c/d/acde8178015e1c715f97d6fc1985cc2f.png) . So if this rotation should be presented as a quaternion,
. So if this rotation should be presented as a quaternion, 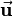 has to equal
has to equal ![[1\ 0\ 0]^T](/wiki/robotics/images/math/a/c/d/acde8178015e1c715f97d6fc1985cc2f.png) . Accordingly the three principal rotations can be described by the following quaternions:
. Accordingly the three principal rotations can be described by the following quaternions:
Assume two rotations are composed as
If two rotations are applied on a vector 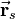 , one rotation is executed first and then the second rotation is applied on the intermediate result
, one rotation is executed first and then the second rotation is applied on the intermediate result 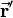 of the first rotation. Using rotation matrices this looks as follows:
of the first rotation. Using rotation matrices this looks as follows:
The corresponding quaternions 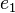 and
and 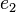 for the two rotations can be computed as explained above and in Rotations using quaternions. So the first quaternion rotation leads to
for the two rotations can be computed as explained above and in Rotations using quaternions. So the first quaternion rotation leads to 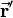 and is defined as
and is defined as
The second rotation is then applied to 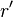 using the second quaternion
using the second quaternion 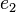 :
:
Since multiplication of quaternions is associative, the order in which the multiplications are solved is not important and does not influence the result. So each the two outer quaternions can be multiplied first:
Following the rule for the conjugate of a product of quaternions this leads to
Thus the rotation 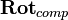 composed by the two rotations
composed by the two rotations 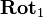 and
and 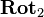 is equivalent to a quaternion
is equivalent to a quaternion 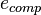 equal to the product of the two corresponding quaternions
equal to the product of the two corresponding quaternions 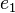 and
and 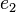 :
:
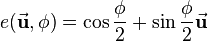
![\begin{align}
e(x,\alpha) &= \cos{\frac{\alpha}{2}} \oplus \sin{\frac{\alpha}{2}} \left[\begin{array}{c}1\\0\\0\end{array}\right] &= \cos{\frac{\alpha}{2}} &+ \sin{\frac{\alpha}{2}} i \\
e(y,\beta) &= \cos{\frac{\beta}{2}} \oplus \sin{\frac{\beta}{2}} \left[\begin{array}{c}0\\1\\0\end{array}\right] &= \cos{\frac{\beta}{2}} &+ \sin{\frac{\beta}{2}} j \\
e(z,\gamma) &= \cos{\frac{\gamma}{2}} \oplus \sin{\frac{\gamma}{2}} \left[\begin{array}{c}0\\0\\1\end{array}\right] &= \cos{\frac{\gamma}{2}} &+ \sin{\frac{\gamma}{2}} k
\end{align}](/wiki/robotics/images/math/4/6/2/4622ef0433f4a945d425ee0f41df8611.png)