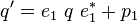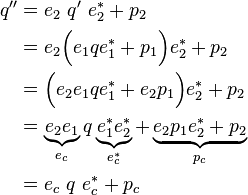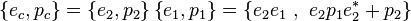Difference between revisions of "Realization of transformations"
| Line 14: | Line 14: | ||
q' = e\ q\ e^*+ p | q' = e\ q\ e^*+ p | ||
</math> | </math> | ||
| + | |||
| + | |||
| + | ---- | ||
| + | |||
Assume a pure translation is to be described using the above notation. Thus the rotation quaternion <math>e</math> describes a rotation with an angle <math>\phi=0^\circ</math> which is actually no rotation at all. According to [[Rotations using quaternions]] <math>e</math> is defined as: | Assume a pure translation is to be described using the above notation. Thus the rotation quaternion <math>e</math> describes a rotation with an angle <math>\phi=0^\circ</math> which is actually no rotation at all. According to [[Rotations using quaternions]] <math>e</math> is defined as: | ||
:<math> | :<math> | ||
| − | + | e_t(\vec{\mathbf{u}},0^\circ)=\cos{0^\circ} + \sin{0^ \circ}\vec{\mathbf{u}} = 1+0\cdot\vec{\mathbf{u}} = 1 | |
</math> | </math> | ||
The rotation axis <math>\vec{\mathbf{u}}</math> can be any arbitrary unit vector as the sine of <math>0^\circ</math> is zero. So <math>e</math> of a pure translation is always just <math>1</math>. | The rotation axis <math>\vec{\mathbf{u}}</math> can be any arbitrary unit vector as the sine of <math>0^\circ</math> is zero. So <math>e</math> of a pure translation is always just <math>1</math>. | ||
The translation quaternion <math>p</math> has scalar part <math>0</math> and the translation vector <math>\vec{\mathbf{p}}</math> as vector part: | The translation quaternion <math>p</math> has scalar part <math>0</math> and the translation vector <math>\vec{\mathbf{p}}</math> as vector part: | ||
:<math> | :<math> | ||
| − | + | p_t=0\ \oplus\ \left[\begin{array}{c}p_x\\p_y\\p_z\end{array}\right] = p_xi+p_yj+p_zk | |
| + | </math> | ||
| + | A translation by <math>2</math> on the <math>y</math>-axis for example would be | ||
| + | :<math> | ||
| + | \mathbf{Trans}(y,2) \eqiv \left\{1,2j\right\} | ||
</math> | </math> | ||
Revision as of 16:54, 15 October 2015
| ← Back: Composition of rotations | Overview: Quaternions | Next: ??? → |
Quaternion notation for general transformations
Up to now transformations have been defined by homogeneous matrices combining a rotation matrix  and a translation vector
and a translation vector 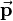 . Now a new notation is introduced to represent a transformation using two quaternions
. Now a new notation is introduced to represent a transformation using two quaternions  and
and 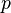 :
:
The quaternion  is equivalent to
is equivalent to  and describes the rotation while
and describes the rotation while 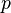 is defined as
is defined as 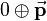 and so equivalent to the translation.
and so equivalent to the translation.
Applying such a transformation to a quaternion 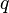 is done by first rotating
is done by first rotating 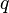 with
with  corresponding to the rotation equation and then adding
corresponding to the rotation equation and then adding 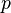 :
:
Assume a pure translation is to be described using the above notation. Thus the rotation quaternion  describes a rotation with an angle
describes a rotation with an angle 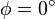 which is actually no rotation at all. According to Rotations using quaternions
which is actually no rotation at all. According to Rotations using quaternions  is defined as:
is defined as:
The rotation axis 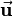 can be any arbitrary unit vector as the sine of
can be any arbitrary unit vector as the sine of  is zero. So
is zero. So  of a pure translation is always just
of a pure translation is always just 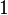 .
The translation quaternion
.
The translation quaternion 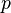 has scalar part
has scalar part 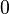 and the translation vector
and the translation vector 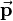 as vector part:
as vector part:
A translation by 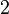 on the
on the 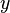 -axis for example would be
-axis for example would be
- Failed to parse (unknown function "\eqiv"): \mathbf{Trans}(y,2) \eqiv \left\{1,2j\right\}
Combination of transformations
It is known that a combination of transformations is defined as:
But how can the two quaternions 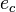 and
and 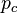 of the quaternion notation be calculated based on the quaternions of individual transformations? The first transformation leads to
of the quaternion notation be calculated based on the quaternions of individual transformations? The first transformation leads to
Now the second transformation is applied on  . The resulting equation can be solved using the distributive law for quaternions to determine
. The resulting equation can be solved using the distributive law for quaternions to determine 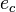 and
and 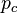 :
:
Thus the combination of two transformations can be denoted in quaternion notation as
Using the knowledge about addition of quaternions and rotations and composition of rotations using quaternions this can directly be determined regarding the homogeneous transformation matrix 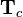 and its rotational and translational components
and its rotational and translational components 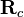 and
and 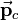 .
.
![\mathbf{T} = \left[\begin{array}{cccc} & & & \\ & \mathbf{R} & & \vec{\mathbf{p}} \\ & & & \\ 0 & 0 & 0 & 1\end{array}\right] \quad \equiv \quad \left\{e,p\right\}](/wiki/robotics/images/math/6/6/1/661d04cca4174d58de7984920f826fb3.png)

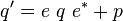
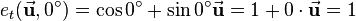
![p_t=0\ \oplus\ \left[\begin{array}{c}p_x\\p_y\\p_z\end{array}\right] = p_xi+p_yj+p_zk](/wiki/robotics/images/math/6/4/2/642c50f36aca3936935ef715956ed74c.png)
![\begin{align}
\mathbf{T}_c = \mathbf{T}_2\mathbf{T}_1 =
\left[\begin{array}{cccc} & & & \\ & \mathbf{R}_2\mathbf{R}_1 & & \vec{\mathbf{p}}_2+\mathbf{R}_2\vec{\mathbf{p}}_1 \\ & & & \\ 0 & 0 & 0 & 1\end{array}\right]
=
\left[\begin{array}{cccc} & & & \\ & \mathbf{R}_c & & \vec{\mathbf{p}}_c \\ & & & \\ 0 & 0 & 0 & 1\end{array}\right]
\quad \equiv \quad
\left\{e_c,p_c\right\}=\left\{e_2,p_2\right\}\left\{e_1,p_1\right\}
\end{align}](/wiki/robotics/images/math/8/b/c/8bc75145f54c5ab026e992e40f2a1842.png)