Difference between revisions of "Realization of transformations"
From Robotics
| Line 1: | Line 1: | ||
{{Navigation|before=[[Composition of rotations]]|overview=[[Quaternions]]|next=[[???]]}} | {{Navigation|before=[[Composition of rotations]]|overview=[[Quaternions]]|next=[[???]]}} | ||
| + | ===Quaternion notation for general transformations=== | ||
Up to now transformations have been defined by homogeneous matrices combining a rotation matrix <math>\mathbf{R}</math> and a translation vector <math>\vec{\mathbf{p}}</math>. Now a new notation is introduced to represent a transformation using two quaternions <math>e</math> and <math>p</math>: | Up to now transformations have been defined by homogeneous matrices combining a rotation matrix <math>\mathbf{R}</math> and a translation vector <math>\vec{\mathbf{p}}</math>. Now a new notation is introduced to represent a transformation using two quaternions <math>e</math> and <math>p</math>: | ||
:<math> | :<math> | ||
Revision as of 16:02, 15 October 2015
| ← Back: Composition of rotations | Overview: Quaternions | Next: ??? → |
Quaternion notation for general transformations
Up to now transformations have been defined by homogeneous matrices combining a rotation matrix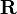 
and a translation vector 
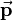. Now a new notation is introduced to represent a transformation using two quaternions 
and 
:
![\mathbf{T} = \left[\begin{array}{cccc} & & & \\ & \mathbf{R} & & \vec{\mathbf{p}} \\ & & & \\ 0 & 0 & 0 & 1\end{array}\right] \equiv \left\{e,p\right\}](/wiki/robotics/images/math/3/0/1/301a5ffd539de858c0981e0180640b3f.png)
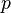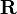The quaternion is equivalent to and describes the rotation while 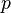is defined as 
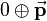and so equivalent to the translation.
Applying such a transformation to a quaternion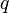 
is done by first rotating 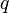with corresponding to the rotation equation and then adding :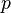
Combination of transformations
It is known that a combination of transformations is defined as:
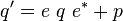
![\begin{align}
\mathbf{T}_c = \mathbf{T}_2\mathbf{T}_1 =
\left[\begin{array}{cccc} & & & \\ & \mathbf{R}_2\mathbf{R}_1 & & \vec{\mathbf{p}}_2+\mathbf{R}_2\vec{\mathbf{p}}_1 \\ & & & \\ 0 & 0 & 0 & 1\end{array}\right]
=
\left[\begin{array}{cccc} & & & \\ & \mathbf{R}_c & & \vec{\mathbf{p}}_c \\ & & & \\ 0 & 0 & 0 & 1\end{array}\right]
\end{align}](/wiki/robotics/images/math/4/d/6/4d6ffbb02d66c18b5fb0b972fad4b82a.png)
