Difference between revisions of "Matrix inversion"

From Robotics
Jump to: navigation, search
Line 7: Line 7:
 
<math>det(\mathbf{A})\ne0</math><br/><br/>
 
<math>det(\mathbf{A})\ne0</math><br/><br/>
 
Otherwise the matrix is called singular. <br/><br/>
 
Otherwise the matrix is called singular. <br/><br/>
−
   '''Example:''' <br/>
+
    
−
  <math>
+
Before determining the inverse of a matrix it is always useful to compute the determinant and check whether the matrix is regular or singular. If it is singular it is not possible to determine the inverse because there is no inverse. For 3-by-3 and smaller matrices there are simple formulas to compute the determinant. To compute the determinant of larger matrices the following paragraph describes an example formula for a 4-by-4 matrix.<br/><br/>
 +
To determine the inverse of a matrix there are several alternatives. Two of the common procedures are the Gauß-Jordan-Algorithm and the Adjugate Formula that are explained afterwards.
 +
 
 +
# [[Minors and cofactors]]
 +
# [[Computing the determinant of a 4-by-4 matrix]]
 +
# [[Gauß-Jordan-Algorithm]]
 +
# [[Adjugate Formula]]
 +
 
 +
{{Example
 +
|Title=inverse of matrix
 +
|Contents=
 +
<math>
 
\mathbf{A}_e  =  
 
\mathbf{A}_e  =  
 
\left[\begin{array}{cccc}
 
\left[\begin{array}{cccc}
Line 25: Line 36:
 
\end{array}\right]
 
\end{array}\right]
 
</math><br/><br/>
 
</math><br/><br/>
−
  <math>\begin{align}
+
<math>\begin{align}
 
\mathbf{A}_e\mathbf{A}_e^{-1}  &=  
 
\mathbf{A}_e\mathbf{A}_e^{-1}  &=  
 
\left[\begin{array}{cccc}
 
\left[\begin{array}{cccc}
Line 52: Line 63:
 
\end{array}\right]=
 
\end{array}\right]=
 
\mathbf{I}_n
 
\mathbf{I}_n
−
\end{align}</math>
+
\end{align}</math>}}
−
<br/>
 
−
Before determining the inverse of a matrix it is always useful to compute the determinant and check whether the matrix is regular or singular. If it is singular it is not possible to determine the inverse because there is no inverse. For 3-by-3 and smaller matrices there are simple formulas to compute the determinant. To compute the determinant of larger matrices the following paragraph describes an example formula for a 4-by-4 matrix.<br/><br/>
 
−
To determine the inverse of a matrix there are several alternatives. Two of the common procedures are the Gauß-Jordan-Algorithm and the Adjugate Formula that are explained afterwards.
 
−
 
 
−
# [[Minors and cofactors]]
 
−
# [[Computing the determinant of a 4-by-4 matrix]]
 
−
# [[Gauß-Jordan-Algorithm]]
 
−
# [[Adjugate Formula]]
 

Revision as of 15:25, 9 May 2014

This article describes the inversion of matrices. It starts with a short explanation of what the inverse of a matrix actually is. Afterwards subarticles present some matrix features and two different approaches to compute the inverse of a matrix based on these features.

The inverse of an n-by-n square matrix 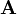\mathbf{A} is denoted as 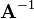\mathbf{A}^{-1} and defined such that

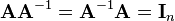
\mathbf{A}\mathbf{A}^{-1}=\mathbf{A}^{-1}\mathbf{A}=\mathbf{I}_n

where 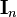\mathbf{I}_n is the n-by-n identity matrix.
Prerequesite for the inversion is, that 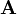\mathbf{A} is an n-by-n square matrix and that 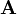\mathbf{A} is regular. Regular means that the row and column vectors are linearly independent and so the determinant is nonzero:

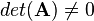
det(\mathbf{A})\ne0

Otherwise the matrix is called singular.

Before determining the inverse of a matrix it is always useful to compute the determinant and check whether the matrix is regular or singular. If it is singular it is not possible to determine the inverse because there is no inverse. For 3-by-3 and smaller matrices there are simple formulas to compute the determinant. To compute the determinant of larger matrices the following paragraph describes an example formula for a 4-by-4 matrix.

To determine the inverse of a matrix there are several alternatives. Two of the common procedures are the Gauß-Jordan-Algorithm and the Adjugate Formula that are explained afterwards.

  1. Minors and cofactors
  2. Computing the determinant of a 4-by-4 matrix
  3. Gauß-Jordan-Algorithm
  4. Adjugate Formula
Example: inverse of matrix

\mathbf{A}_e = \left[\begin{array}{cccc} 1 & 2 & 0 & 0\\ 3 & 0 & 1 & 1\\ 0 & 1 & 0 & 0\\ 0 & 0 & 2 & 1 \end{array}\right] ,\quad \mathbf{A}_e^{-1} = \left[\begin{array}{cccc} 1 & 0 & -2 & 0\\ 0 & 0 & 1 & 0\\ 3 & -1 & -6 & 1\\ -6 & 2 & 12 & -1 \end{array}\right]

\begin{align} \mathbf{A}_e\mathbf{A}_e^{-1} &= \left[\begin{array}{cccc} 1 & 2 & 0 & 0\\ 3 & 0 & 1 & 1\\ 0 & 1 & 0 & 0\\ 0 & 0 & 2 & 1 \end{array}\right]\cdot \left[\begin{array}{cccc} 1 & 0 & -2 & 0\\ 0 & 0 & 1 & 0\\ 3 & -1 & -6 & 1\\ -6 & 2 & 12 & -1 \end{array}\right]\\&= \left[\begin{array}{cccc} 1+0+0+0 & 0+0+0+0 & -2+2+0+0 & 0+0+0+0\\ 3+0+3-6 & 0+0-1+2 & -6+0-6+12 & 0+0+1-1\\ 0+0+0+0 & 0+0+0+0 & 0+1+0+0 & 0+0+0+0\\ 0+0+6-6 & 0+0-2+2 & 0+0-12+12 & 0+0+2-1 \end{array}\right]\\&= \left[\begin{array}{cccc} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{array}\right]= \mathbf{I}_n \end{align}

Retrieved from "https://getwww.uni-paderborn.de/wiki/robotics/index.php?title=Matrix_inversion&oldid=19"