Difference between revisions of "Inverse transformation"
From Robotics
| Line 11: | Line 11: | ||
\end{array}\right] | \end{array}\right] | ||
</math> | </math> | ||
| − | Multiplication with <math>\mathbf{T}</math> corresponds to applying the rotation matrix <math>\mathbf{R}</math> first and then translating the coordinates by <math>\vec{\mathbf{p}}</math> | + | Multiplication with <math>\mathbf{T}</math> corresponds to applying the rotation matrix <math>\mathbf{R}</math> first and then translating the coordinates by <math>\vec{\mathbf{p}}</math>:<br/> |
| + | :<math> | ||
| + | \vec{\mathbf{q}}_1= | ||
| + | \mathbf{T} \cdot \vec{\mathbf{q}}_0 = | ||
| + | \mathbf{R}\cdot \vec{\mathbf{q}}_0 + \vec{\mathbf{p}} | ||
| + | </math> | ||
[[Category:Article]] | [[Category:Article]] | ||
[[Category:Transformations]] | [[Category:Transformations]] | ||
Revision as of 13:45, 17 June 2014
| ← Back: Combinations of transformations | Overview: Transformations | Next: ??? → |
A general homogeneous transformation matrix 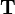 for three-dimensional space consists of a 3-by-3 rotation matrix
for three-dimensional space consists of a 3-by-3 rotation matrix 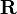 and a 3-by-1 translation vector
and a 3-by-1 translation vector 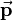 combined with the last row of the identity matrix:
combined with the last row of the identity matrix:
Multiplication with 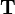 corresponds to applying the rotation matrix
corresponds to applying the rotation matrix 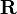 first and then translating the coordinates by
first and then translating the coordinates by 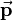 :
:
![\mathbf{T}=
\left[\begin{array}{ccc|c}
& & & \\
& \mathbf{R} & & \vec{\mathbf{p}}\\
& & & \\ \hline
0 & 0 & 0 & 1
\end{array}\right]](/wiki/robotics/images/math/1/3/2/1327593f05795df92e5c12f1a1a27f84.png)