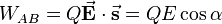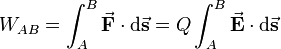Dot product
| ← Back: Simple arithmetic operations | Overview: Vector algebra | Next: Cross product → |
The dot product of two vectors results in a scalar value and is defined as
where 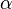 describes the angle between the two vectors which ranges from
describes the angle between the two vectors which ranges from 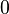 to
to 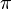 (see figure). The dot product is denoted with a simple point between the vectors or without any sign.
(see figure). The dot product is denoted with a simple point between the vectors or without any sign.
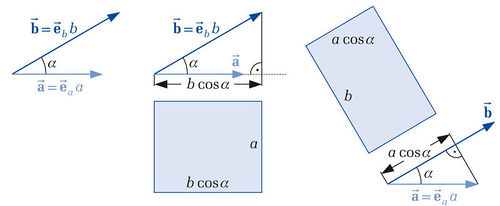
Regarding the right side of the above equation, the following correlation can be noted: If you project the vector 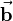 on the vector
on the vector 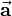 , you get the distance
, you get the distance 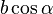 . As a consequence the result of the dot product can be seen as the acreage of a rectangle with the side legths
. As a consequence the result of the dot product can be seen as the acreage of a rectangle with the side legths 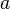 and
and 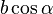 . The projection can also be done contrariwise (projection of vector
. The projection can also be done contrariwise (projection of vector 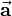 on the direction of vector
on the direction of vector 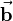 ). So that you get the distance
). So that you get the distance 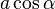 . Die Multiplikation dieses Terms mit
. Die Multiplikation dieses Terms mit 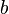 führt zu einem Rechteck mit identischem Flächeninhalt aber einem anderen Seitenverhältnis (siehe Abbildung).
führt zu einem Rechteck mit identischem Flächeninhalt aber einem anderen Seitenverhältnis (siehe Abbildung).
Eine weitere Möglichkeit zur Bestimmung des Skalarprodukts ist dadurch gegeben, dass man zunächst die korrespondierenden Komponenten multipliziert und anschließend aufsummiert:
Ganz allgemein - zum Beispiel wenn man es nicht mit Vektoren aus dem kartesischen Koordinatensystem zu tun hat - lässt sich das Skalarprodukt wie folgt bestimmen:
Anhand der beschriebenen Zusammenhänge zeigt sich, dass das Skalarprodukt dem Kommutativgesetz genügt. Somit gilt:
Weiterhin ergeben sich einige Sonderfälle, die im technischen Kontext häufig zu Vereinfachungen führen:
Ein häufiger Anwendungsfall des Skalarprodukts ergibt sich bei dem Begriff der Arbeit. Bewegt man beispielsweise eine Punktladung Bei der Verschiebung der Ladung muss die Coulomb-Kraft Allgemein, also wenn die elektrische Feldstärke nicht homogen und der Weg der Verschiebung von |
Multimedial educational material
|
http://www.mathresource.iitb.ac.in/linear%20algebra/example7.1/index.html Applet: Skalarprodukt zweier Vektoren (engl.) http://www.cs.brown.edu/exploratories/freeSoftware/repository/edu/brown/cs/exploratories/applets/dotProduct/dot_product_java_browser.html Applet: Skalarprodukt zweier Vektoren http://www.mathresource.iitb.ac.in/linear%20algebra/example7.2/index.html Applet: Skalarprodukt zweier Vektoren mit der eingeschlossenen Fläche http://demonstrations.wolfram.com/DotProduct/ Applet: Skalarprodukt zweier Vektoren (engl./ free CDF-Player erforderlich) http://www.math.ethz.ch/~lemuren/public/exercise/linalg/LinearCombinationInR2ETHZ.html Applet: Linearkombination im zweidimensionalem Raum |
Literature
- Kurt Meyberg und Peter Vachenauer, Höhere Mathematik 1: Differential- und Integralrechnung. Vektor- und Matrizenrechnung, 6. Edition (Springer Berlin Heidelberg, 2001)
- Manfred Albach, Grundlagen der Elektrotechnik 1: Erfahrungssätze, Bauelemente, Gleichstromschaltungen, 3. Edition (Pearson Studium, 2011)
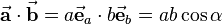
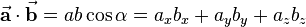
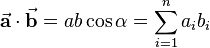
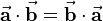
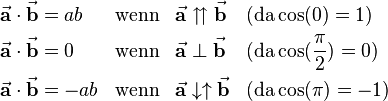
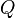 in einem homogenen elektrischen Feld
in einem homogenen elektrischen Feld 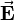 entlang einer geraden Strecke
entlang einer geraden Strecke 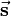 von einem Punkt
von einem Punkt 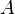 zu einem Punkt
zu einem Punkt 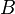 , so lässt sich die dabei aufgewendete Arbeit mit Hilfe des Skalarprodukts wie folgt bestimmen:
, so lässt sich die dabei aufgewendete Arbeit mit Hilfe des Skalarprodukts wie folgt bestimmen:
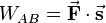
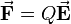 aufgebracht werden, das heißt in diesem Fall ergibt sich der folgende Zusammenhang:
aufgebracht werden, das heißt in diesem Fall ergibt sich der folgende Zusammenhang: