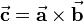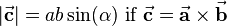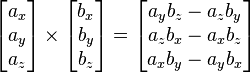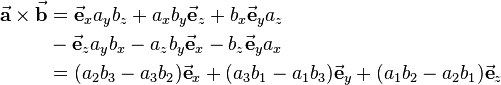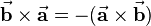Cross product

← Back: Dot product

Overview: Vector algebra

Next: Matrices →

The cross product of two vectors is denoted with an 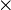$\times$. The cross product of vector 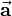$\vec{\mathbf{a}}$ and vector 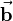$\vec{\mathbf{b}}$ results in a new vector

$\vec{\mathbf{c}} = \vec{\mathbf{a}} \times \vec{\mathbf{b}}$

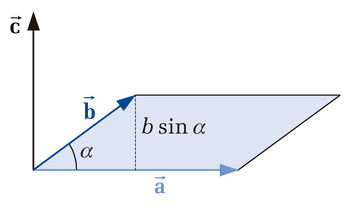
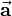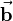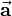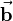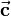that is perpendicular to the surface spanned by vectors $\vec{\mathbf{a}}$ and $\vec{\mathbf{b}}$ (see figure). Furthermore the three vectors $\vec{\mathbf{a}}$, $\vec{\mathbf{b}}$ and $\vec{\mathbf{c}}$ build a rectangular coordinate system based on the right-hand rule. 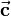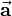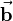The magnitude of vector $\vec{\mathbf{c}}$ equals the area of the parallelogram spanned by $\vec{\mathbf{a}}$ and $\vec{\mathbf{b}}$ and is calculated as follows:

$|\vec{\mathbf{c}}| = a b \sin(\alpha)\ \text{if}\ \vec{\mathbf{c}} = \vec{\mathbf{a}} \times \vec{\mathbf{b}}$

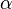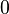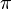Dabei bezeichnet $\alpha$ den Winkel, der von den beiden Vektoren eingeschlossen wird und Werte zwischen $0$ und $\pi$ annehmen kann (siehe Abbildung). Weiterhin gilt es zu beachten, dass das Vektorprodukt ausschließlich für den dreidimensionalen euklidischen Vektorraum definiert ist. Rechnerisch gilt der folgende Zusammenhang:

$\begin{align} \begin{bmatrix} a_x\\ a_y\\ a_z\end{bmatrix} \times \begin{bmatrix} b_x\\ b_y\\ b_z\end{bmatrix} = \begin{bmatrix} a_y b_z - a_z b_y\\ a_z b_x - a_x b_z\\ a_x b_y - a_y b_x\end{bmatrix} \end{align}$

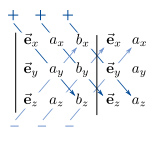
Als Merkhilfe für diesen Zusammenhang eignet sich die Regel von Sarrus: Entsprechend der Abbildung werden dabei die Einheitsvektoren des kartesischen Koordinatensystems in eine erste Spalte und die anderen beiden Vektoren in eine zweite und dritte Spalte geschrieben. Auf diese Weise erhält man eine Matrix, deren ersten beiden Spalten nun erneut rechts neben diese Matrix geschrieben werden. Nun führt man die Multiplikationen und Additionen wie in der Abbildung gezeigt aus und erhält:

$\begin{align} \vec{\textbf{a}} \times \vec{\textbf{b}} &= \vec{\textbf{e}}_x a_y b_z + a_x b_y \vec{\textbf{e}}_z + b_x \vec{\textbf{e}}_y a_z\\ & -\vec{\textbf{e}}_z a_y b_x - a_z b_y \vec{\textbf{e}}_x - b_z \vec{\textbf{e}}_y a_x\\ &= (a_2 b_3 - a_3 b_2) \vec{\textbf{e}}_x + (a_3 b_1 - a_1 b_3) \vec{\textbf{e}}_y + (a_1 b_2 - a_2 b_1) \vec{\textbf{e}}_z \end{align}$

Aus mathematischer Sicht bestimmt man auf diese Weise die Determinante der genannten Matrix. Anhand der beschriebenen Zusammenhänge zeigt sich, dass das Skalarprodukt nicht dem Kommutativgesetz genügt. Stattdessen gilt:

$\vec{\textbf{b}} \times \vec{\textbf{a}} = -(\vec{\textbf{a}} \times \vec{\textbf{b}})$

Weiterhin ergeben sich einige Sonderfälle, die im technischen Kontext häufig zu Vereinfachungen führen:

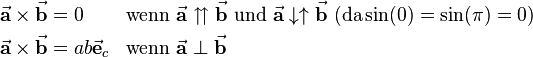$\begin{align} \vec{\textbf{a}}\times\vec{\textbf{b}} &= 0 &\text{wenn}&\ \vec{\textbf{a}} \upuparrows \vec{\textbf{b}}\ \text{und}\ \vec{\textbf{a}} \downarrow\uparrow \vec{\textbf{b}}\ (\text{da} \sin(0) = \sin(\pi) = 0)\\ \vec{\textbf{a}}\times\vec{\textbf{b}} &= a b \vec{\textbf{e}}_c &\text{wenn}&\ \vec{\textbf{a}} \perp \vec{\textbf{b}} \end{align}$<br/<

Multimedial educational material

http://www.surendranath.org/Applets/Math/VectorProduct/VP.html Applet: Cross product of two vectors in cartesian and polar coordinates http://demonstrations.wolfram.com/CrossProductOfVectorsInTheYZPlane/ Applet: Cross product of two vectors in the yz-plane

Literatur

• Manfred Albach, Grundlagen der Elektrotechnik 1: Erfahrungssätze, Bauelemente, Gleichstromschaltungen, 3. Edition (Pearson Studium, 2011)
• Kurt Meyberg und Peter Vachenauer, Höhere Mathematik 1: Differential- und Integralrechnung. Vektor- und Matrizenrechnung, 6. Edition (Springer Berlin Heidelberg, 2001)
• Wolfgang Pavel und Ralf Winkler, Mathematik für Naturwissenschaftler, 1. Edition (Pearson Studium, 2007)