Combinations of transformations

← Back: Homogeneous coordinates

Overview: Transformations

Next: Inverse transformation →

In the previous subarticle homogeneous coordinates and transformation matrices for translation and rotation around the three axes are introduced:

$\mathbf{Trans}(p_x,p_y,p_z), \quad\mathbf{Rot}(x,\varphi), \quad \mathbf{Rot}(y,\varphi), \quad\mathbf{Rot}(z,\varphi)$

These transformation matrices can be combined by multiplying them. The most important thing that has to be considered combining transformations, is the order of the transformations. Different orders lead to different results. Descriptively seen, rotation is always applied around the origin or around axis intersecting with the origin, respectively. So the rotational part is depending on the respective input coordinates. Different orders of transformations result in different input coordinates for each transformation.

The following example shows descriptively as well as computationally, that the order of transformations is important. Consider a translation matrix 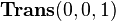$\mathbf{Trans}(0,0,1)$ and a rotation matrix 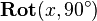$\mathbf{Rot}(x,90^\circ)$. The upper three subfigures on the right

the general homogeneous transformation matrix $\mathbf{T}$ were introduced. $\mathbf{T}$ consists of a rotation matrix and a translation vector:

$\mathbf{T}= \left[\begin{array}{ccc|c} & & & \\ & \mathbf{R} & & \vec{\mathbf{p}}\\ & & & \\ \hline 0 & 0 & 0 & 1 \end{array}\right]$

As shown in the subarticle homogeneous coordinates, multiplication of $\mathbf{T}$ with a vector corresponds to rotating the coordinates first and then adding the translation vector.

Pre-/Post-...

transformation matrices for translation and rotation around the three axes are introduced:

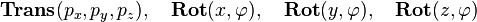
$\mathbf{Trans}(p_x,p_y,p_z), \quad\mathbf{Rot}(x,\varphi), \quad \mathbf{Rot}(y,\varphi), \quad\mathbf{Rot}(z,\varphi)$