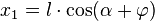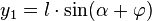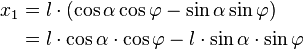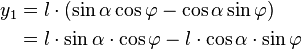Difference between revisions of "Rotation"
From Robotics
| Line 30: | Line 30: | ||
<math>\begin{align} | <math>\begin{align} | ||
x_1&=l\cdot(\cos\alpha\cos\varphi-\sin\alpha\sin\varphi) \\ | x_1&=l\cdot(\cos\alpha\cos\varphi-\sin\alpha\sin\varphi) \\ | ||
| − | &=l\cos\alpha\cdot\cos\varphi-l\sin\alpha\cdot\sin\varphi | + | &=l\cdot\cos\alpha\cdot\cos\varphi-l\cdot\sin\alpha\cdot\sin\varphi |
\end{align}</math> | \end{align}</math> | ||
</td> | </td> | ||
<td width="350px" valign="center" align="left"> | <td width="350px" valign="center" align="left"> | ||
| − | <math> | + | <math>\begin{align} |
| − | y_1=l\cdot(\sin\alpha\cos\varphi-\cos\alpha\sin\varphi) | + | y_1&=l\cdot(\sin\alpha\cos\varphi-\cos\alpha\sin\varphi) \\ |
| − | </math> | + | &=l\cdot\sin\alpha\cdot\cos\varphi-l\cdot\cos\alpha\cdot\sin\varphi |
| + | \end{align}</math> | ||
| + | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
Revision as of 13:27, 30 May 2014
| ← Back: Scaling | Overview: Transformations | Next: Homogeneous coordinates → |
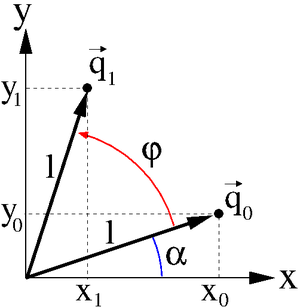
Rotation is a transformation where the coordinates are rotated around the origin of the coordinate system. In this article rotation is first described for two dimensions.
The figure on the right shows an example, where the vector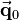 
is rotated by 
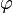around the origin, what results in vector 
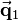. The length of the vector 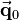is assumed as 
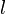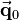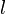and so the length of is as well. The initial angle of 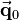relative to the x-axis is 
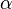. Hence the resulting coordinates 
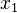and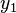 
can be computed as follows:
|
|
|
Using the addition theorems of sine and cosine leads to:
|
|
|
