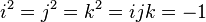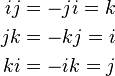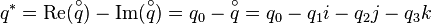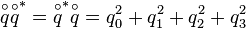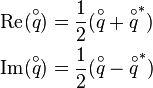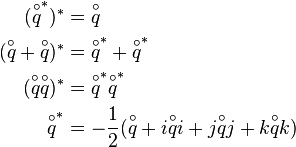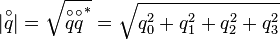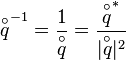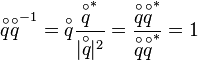Basic properties of quaternions

← Back: Quaternions

Overview: Quaternions

Next: Pure and unit quaternions →

Imaginary part

The imaginary units of a quaternion are defined as follows:

$i^2 = j^2 = k^2 = ijk = -1$

Unlike the multiplication of real or complex numbers, the multiplication is not commutative:

$\begin{align} ij &= -ji = k \\ jk &= -kj = i \\ ki &= -ik = j \end{align}$

Conjugate

The conjugate 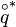$\overset{\circ}{q}^*$ of a quaternion 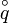$\overset{\circ}{q}$ is obtained by negating the imaginary or vector part, respectively:

$q^*= \text{Re}(\overset{\circ}{q}) - \text{Im}(\overset{\circ}{q}) = q_0-\overset{\circ}{q} = q_0 - q_1i - q_2j - q_3k$

Multiplying a quaternion with its conjugate like described in the subarticle about multiplication of quaternions consequently leads to

$\overset{\circ}{q}\overset{\circ}{q}^* = \overset{\circ}{q}^*\overset{\circ}{q} =q_0^2 + q_1^2 + q_2^2 + q_3^2$

The conjugate can be used to easily determine the real part and the imaginary part of a quaternion:

$\begin{align} \text{Re}(\overset{\circ}{q}) &= \frac{1}{2}(\overset{\circ}{q}+\overset{\circ}{q}^*) \\ \text{Im}(\overset{\circ}{q}) &= \frac{1}{2}(\overset{\circ}{q}-\overset{\circ}{q}^*) \end{align}$

The most important properties of the conjugate are:

$\begin{align} (\overset{\circ}{q}^*)^* &= \overset{\circ}{q} \\ (\overset{\circ}{q}+\overset{\circ}{q})^* &= \overset{\circ}{q}^* + \overset{\circ}{q}^* \\ (\overset{\circ}{q}\overset{\circ}{q})^* &= \overset{\circ}{q}^*\overset{\circ}{q}^* \\ \overset{\circ}{q}^* &= -\frac{1}{2}(\overset{\circ}{q}+i\overset{\circ}{q}i+j\overset{\circ}{q}j+k\overset{\circ}{q}k) \end{align}$

Norm

The norm of a quaternion corresponds to its euclidean length in four-dimensional space and is computed as follows:

$|\overset{\circ}{q}| = \sqrt{\overset{\circ}{q}\overset{\circ}{q}^*} = \sqrt{q_0^2 + q_1^2 + q_2^2 + q_3^2}$

It holds:

$|\overset{\circ}{q}\overset{\circ}{q}| = |\overset{\circ}{q}||\overset{\circ}{q}|$

Inverse

The inverse of a quaternion is defined as follows:

$\overset{\circ}{q}^{-1} = \frac{1}{\overset{\circ}{q}} = \frac{\overset{\circ}{q}^*}{|\overset{\circ}{q}|^2}$

This can be proven by multiplying a quaternion 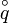$\overset{\circ}{q}$ with its inverse using the definition of the norm:

$\overset{\circ}{q}\overset{\circ}{q}^{-1} = \overset{\circ}{q}\frac{\overset{\circ}{q}^*}{|\overset{\circ}{q}|^2} = \frac{\overset{\circ}{q}\overset{\circ}{q}^*}{\overset{\circ}{q}\overset{\circ}{q}^*} = 1$