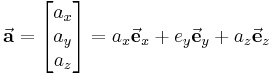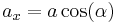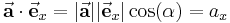Komponentendarstellung von Vektoren

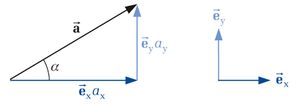
Komponentenzerlegung eines Vektors

Vektorzerlegung

Bestimmung der Komponenten

Betrachtet man beispielsweise einen Vektor $\vec{\textbf{a}}$ im dreidimensionalen kartesischen Koordinatensystem, so lässt sich dieser auch als Summe der Produkte seiner Komponenten und den zugehörigen Einheitsvektoren, die in die Richtungen der jeweiligen Koordinatenachsen zeigen, angeben:

$\vec{\textbf{a}} = \begin{bmatrix} a_x\\ a_y\\ a_z \end{bmatrix} = a_x \vec{\textbf{e}}_{x} + e_y \vec{\textbf{e}}_{y} + a_z \vec{\textbf{e}}_{z}$

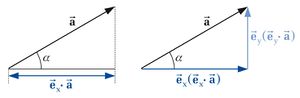
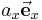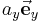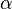Die Gültigkeit dieses Zusammenhangs lässt sich anhand des zweidimensionalen Beispiels in der Abbildung zur Vektorzerlegung nachvollziehen: Bildet man die Summe der beiden Vektoren $a_x \vec{\textbf{e}}_x$ und $a_y \vec{\textbf{e}}_y$, so erhält man wieder den ursprünglichen Vektor $\vec{\textbf{a}}$. Führt man nun wie dargestellt einen Winkel $\alpha$ ein, so lässt sich feststellen, dass sich die Strecke 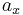$a_x$ mit Hilfe des Kosinus wie folgt bestimmen lässt:

$a_x = a \cos(\alpha)$

Mit Hilfe des Skalarprodukts — geometrisch interpretiert auch weil sich die Strecke 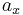$a_x$ bei der Projektion des Vektors $\vec{\textbf{a}}$ auf die parallel zum Einheitsvektor 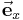$\vec{\textbf{e}}_{x}$ verlaufende Linie ergibt — lässt sich dieser Zusammenhang auch wie folgt ausdrücken:

$\vec{\textbf{a}} \cdot \vec{\textbf{e}}_{x} = |\vec{\textbf{a}}| |\vec{\textbf{e}}_{x}| \cos(\alpha) = a_x$