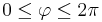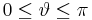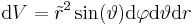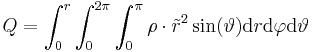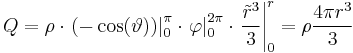Das Volumenintegral
Bei keiner anderen bisher betrachteten Integration ist ihr Nutzen so anschaulich, wie bei der Volumenintegration.
Möchte man z.B. die Masse m eines Körpers bestimmen, dessen Dichte 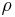 ortsabhängig ist, verwendet man das Volumenenintegral um die Masse zu berechnen.
ortsabhängig ist, verwendet man das Volumenenintegral um die Masse zu berechnen.
Zur Herleitung muss der Körper zunächst in i würfelförmige Teilstücke 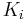 mit i=1,...n zerlegt werden, wobei jedes Würfelstück eine bestimmte Kantenlänge
mit i=1,...n zerlegt werden, wobei jedes Würfelstück eine bestimmte Kantenlänge 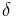 aufweißt. Anschließend multipliziert man das Volumen der Würfelstücke
aufweißt. Anschließend multipliziert man das Volumen der Würfelstücke 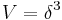 mit der spezifischen Dichte
mit der spezifischen Dichte 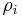 , und summiert alle Produkte über das Volumen auf. So erhält man:
, und summiert alle Produkte über das Volumen auf. So erhält man:
Bildet man nun den Grenzwert, also lässt die Kantenlänge 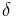 der Würfel gegen 0 gehen, während ihre Anzahl gegen
der Würfel gegen 0 gehen, während ihre Anzahl gegen 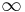 geht, folgt daraus folgende Form des Volumenintegrals:
geht, folgt daraus folgende Form des Volumenintegrals:
auch hier ist die andere Schreibweise möglich:
Gegeben ist die homogene Dichte
Da die Dichte nicht weiter ist, als die Masse pro Volumen, lässt sich die Masse durch die Integration der Dichte über das Volumen des Zylinders berechnen: Dafür benötigt man zunächst das Volumenelement eines Zylinders: Da hier die Integrationsvariable und die Variable in der Funktion gleich sind, setzt man eine Tilde ( Da Da Nicht mehr ganz so einfach wird die Rechnung jedoch wenn Führt man nun die selbe Rechnung durch, ergibt sich: Die Konstante Aus dieser Betrachtung sieht man, das das Volumenintegral unersetzlich ist, sobald irgendeine Abhängigkeit zwischen dem Volumen und der Funktion existiert. |
Gegeben sei eine homogene Raumladung Dazu muss über das gesamte Volumen der Kugel integriert werden. Die Grenzen sind also die maximalen Ausdehnungen der Kugelkoordinaten insbesondere für die Winkel Außerdem muss das Volumenelement in Kugelkoordinatenverwendet werden, dies ergibt sich aus der Symetrie zu:
Eingesetzt folgt daraus: Da |
Multimediale Lehrmaterialien
|
http://demonstrations.wolfram.com/DoubleIntegralForVolume/ Applet: Doppelintegral über ein Volumen mit Hilfe von Unter und Obersummen (engl./ free CDF-Player erforderlich) http://www.surendranath.org/Applets/Electricity/BSLMFACC/BSL.html Applet zum Darstellen des Magnetischen Feldes http://susannealbers.de/pk_applets/efeld/06wissen-physik-efeld.html Applet zu Punktladung und deren Feldlinien und Potenziale |
Hilfreiche Links
|
http://www.tphys.physik.uni-tuebingen.de/muether/physik1/skript/03-02.pdf Bebilderte Beschreibung zum Volumenintegral am Beispiel von Massepunkten http://www-hm.ma.tum.de/integration/course/html/ch2/t/t_parent.htm Verschiedene Anwendungen der Integration http://www.hoever.fh-aachen.de/SS06/mathe/skript/Mathe2-2.pdf Erklärung zum mehrdimensionalen Integrieren http://www.tphys.physik.uni-tuebingen.de/muether/physik1/skript/03-02.pdf Bebilderte Beschreibung zum Volumenintegral am Beispiel von Massepunkten |
| ← Zurück: Das Flächenintegral | Übersicht: Erweiterung der Integralrechnung | Vorwärts: Erweiterung der Integralrechnung → |
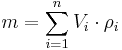
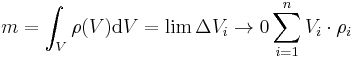
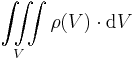
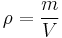 eines Zylinders mit der Höhe l und dem Radius r. Gesucht wird seine Gesamtmasse.
eines Zylinders mit der Höhe l und dem Radius r. Gesucht wird seine Gesamtmasse.
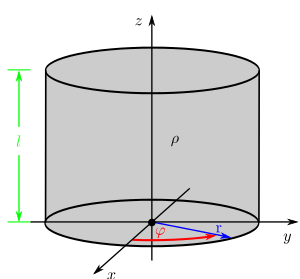
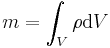
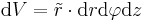
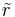 ) über das r, um zu zeigen, dass es sich nicht um das selbe r handelt. Nun setzt man dieses Volumenelement und die Grenzen des Zylinders in die obige Gleichung ein:
) über das r, um zu zeigen, dass es sich nicht um das selbe r handelt. Nun setzt man dieses Volumenelement und die Grenzen des Zylinders in die obige Gleichung ein:
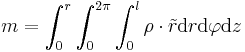
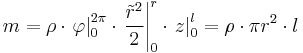
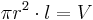 auch das Volumen des Zylinders ist lässt sich hier auch die einfache Form ohne Integral zur Lösung nutzen:
auch das Volumen des Zylinders ist lässt sich hier auch die einfache Form ohne Integral zur Lösung nutzen:
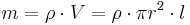
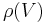 gegeben durch:
gegeben durch:

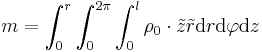
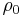 lässt sich wieder vorziehen und das Integral ergibt:
lässt sich wieder vorziehen und das Integral ergibt:
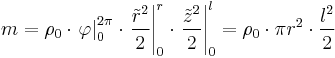
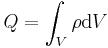
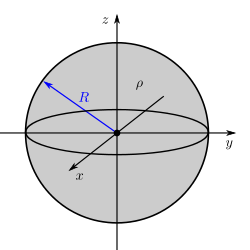
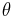 und
und  :
: