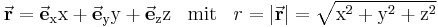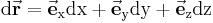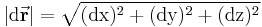Kartesische Koordinaten: Unterschied zwischen den Versionen

Version vom 19. April 2012, 18:24 Uhr

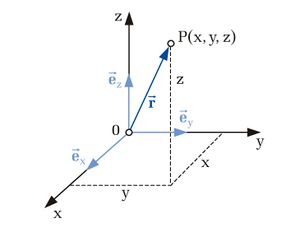
Abbildung 1: Das Kartesische Koordinatensystem

Aus der Schule sollte der einfachste Fall des kartesischen Koordinatensystems bereits hinreichend bekannt sein. In der Elektrotechnik wird es vor allem für planare Systeme verwendet. Betrachtet man zum Beispiel die Kapazität eines Plattenkondensators, empfiehlt es sich, dieses Koordinatensystem zu gebrauchen. Außerdem werden viele abstrakte Größen in dem kartesischen Koordinatensystem dargestellt, beispielsweise die zeitliche Änderung der Spannung, kann man diese auch in das Koordinatensystem eintragen, wobei die x-Achse der Zeit entspricht und die y-Achse der Spannung. Da davon auszugehen ist, dass die meisten sich mit diesem System bereits auskennen, ist diese Seite nur eine kurze Wiederholung der wichtigsten Eigenschaften, um diese auch auf die anderen Koordinatensysteme übetragen zu können:

Eine der wichtigsten Eigenschaften des kartesischen Koordinatensystems ist, dass die Koordinatenachsen, die häufig auch als x-, y-, und z-Achse beschrieben werden, orthogonal zueinander stehen. Im Vergleich zu anderen Koordinatensystemen zeigen hier die Einheitsvektoren 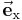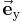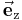$\vec{\textbf{e}}_\mathrm{x}$ , $\vec{\textbf{e}}_\mathrm{y}$ , $\vec{\textbf{e}}_\mathrm{z}$ immer in die selbe Richtung und sind parallel zu den Achsen. Deshalb ist dieses Koordinatensystem intuitiv verständlich.

Außerdem bilden die Achsen zueinander ein Rechtssystem. Hält man die Hand in den Koordinatenursprung (dort, wo sich die Koordinatenachsen schneiden), kann man mit Hilfe der Rechten Handregel1 ihre Richtungen bestimmen. Oder man nutzt die Rechtsschraubenregel, indem man die positive x-Achse auf dem kürzesten Weg in Richtung der positiven y-Achse dreht (d. h. gegen den Uhrzeigersinn). Verschiebt man gleichzeitig die Richtung in die positive z-Achse, erhält man eine Rechtsschraube.

Als Koordinatenflächen erhält man die drei orthogonal zueinander angeordneten Ebenen x = const. (entspricht der y-z-Ebene), y = const. (entspricht der x-z-Ebene) und z = const. (entspricht der x-y-Ebene).

Der Ortsvektor 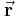$\vec{\textbf{r}}$ des Raumpunkts P wird bezogen auf den Koordinatenursprung 0 mit Hilfe der Länge 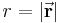$r = \left| \vec{\textbf{r}} \right|$ beschrieben:

\begin{align} \vec{\textbf{r}} & = \vec{\textbf{e}}_\mathrm{x} \mathrm{x} + \vec{\textbf{e}}_\mathrm{y} \mathrm{y} + \vec{\textbf{e}}_\mathrm{z} \mathrm{z} && \text{mit} & r = \left| \vec{\textbf{r}} \right| = \sqrt{\mathrm{x}^2 + \mathrm{y}^2 + \mathrm{z}^2} \end{align}

Abbildung 2: Vektorielles Wegelement

Für die meisten Kurvenintegrale wird das differentielle Wegelement 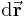$\mathrm{d} \vec{\textbf{r}}$ benötigt. Dabei ist das differentielle Wegelement nichts anderes als die differentielle Änderung des Ortsvektors beim Fortschreiten vom Punkt P(x,y,z) um die elementaren Strecken dx, dy, dz. Dadurch wird die Richtung der Kurve in einem bestimmten Punkt angegeben.

\mathrm{d} \vec{\textbf{r}} = \vec{\textbf{e}}_\mathrm{x} \mathrm{dx} + \vec{\textbf{e}}_\mathrm{y} \mathrm{dy} + \vec{\textbf{e}}_\mathrm{z} \mathrm{dz}

die Länge des Wegelements ergibt sich durch Berechnung des Betrages des differentiellen Wegelements:

\left| \mathrm{d} \vec{\textbf{r}} \right| = \sqrt{(\mathrm{dx})^2 + (\mathrm{dy})^2 + (\mathrm{dz})^2}

Multimediale Lehrmaterialien

http://www.mathe-online.at/mathint/zeich/applet_b_kartes.htmlApplet: Kartesische Koordinaten im zweidimensionalem Raum

http://www.mathe-online.at/mathint/zeich/applet_b_schief.html Applet: Schiefwinkliges Koordinatensystem im zweidimensionalem Raum

http://www.kleemannschule.de/de/unterricht/mathematik/punkt3D.html Applet: Ein Punkt im dreidimensionalem Raum mit seinen Ortsvektoren

Hilfreiche Links

http://cnx.org/content/m13600/latest/ Übersicht zu verschiedenen Koordinatensystemen

← Zurück: Orthogonale Koordinatensysteme:Übersicht

Übersicht: Orthogonale Koordinatensysteme

Vorwärts: Zylinderkoordinaten →

@@ Zeile 31: / Zeile 31: @@
 </figure>
-Für die meisten Kurvenintegrale wird das differentielle Wegelement <math>\mathrm{d} \vec{\textbf{r}}</math> benötigt. Dabei ist das differentielle Wegelement nichts anderes als die differentielle Änderung des Ortsvektors beim Fortschreiten vom Punkt P(x,y,z) um die elementaren Strecken dx, dy, dz. Dadurch wird die ''Richtung'' der Kurve in einem bestimmten Punkt angegeben.
+Für die meisten Kurvenintegrale wird das [[differentielle Wegelement]] <math>\mathrm{d} \vec{\textbf{r}}</math> benötigt. Dabei ist das differentielle Wegelement nichts anderes als die differentielle Änderung des Ortsvektors beim Fortschreiten vom Punkt P(x,y,z) um die elementaren Strecken dx, dy, dz. Dadurch wird die ''Richtung'' der Kurve in einem bestimmten Punkt angegeben.
 :<math>
 \mathrm{d} \vec{\textbf{r}} =

Kartesische Koordinaten: Unterschied zwischen den Versionen

Version vom 19. April 2012, 18:24 Uhr

Navigationsmenü

Meine Werkzeuge

Namensräume

Varianten

Ansichten

Mehr

Suche

Navigation

Werkzeuge