Difference between revisions of "Gauß-Jordan-Algorithm"
| Line 61: | Line 61: | ||
|Contents= | |Contents= | ||
This example describes the computation of the inverse of the transform matrix <math>^R\mathbf{T}_N</math> that is introduced in the script on page 3-37 and used on the following pages. | This example describes the computation of the inverse of the transform matrix <math>^R\mathbf{T}_N</math> that is introduced in the script on page 3-37 and used on the following pages. | ||
| − | <br/><math>\begin{align} | + | <br/> |
| + | :<math>\begin{align} | ||
\mathbf{A}_e = | \mathbf{A}_e = | ||
&\left[\begin{array}{cccc} | &\left[\begin{array}{cccc} | ||
Revision as of 15:19, 22 May 2014
| ← Back: Matrix inversion | Overview: Matrix inversion | Next: Adjugate Formula → |
The Gauß-Jordan-Algorithm was developed to solve systems of linear equations. But it can also be used to determine the inverse of an n-by-n square matrix.
The algorithm is based on the formula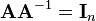 
. First the block matrix 
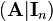is build. On this matrix the Gauß-Jordan-Algorithm is applied. By using various conversion steps like interchanging of rows and addtition of factorized rows to other rows the block matrix is converted so that the left block equals the identity matrix 
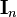. The right block then corresponds to the inverse of 
.
 Example: Gauß-Jordan-Algorithm for a 2-by-2 matrix
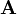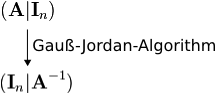
This example describes the application of the Gauß-Jordan-Algorithm to compute the inverse of |
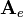, which is already used for the example in the main article of ![\begin{align}
\mathbf{A}_e =
&\left[\begin{array}{cc}
2 & 3\\
1 & 2
\end{array}\right]\\ \\
(\mathbf{A}_e|\mathbf{I}_2) =
&\left[\begin{array}{cc|cc}
2 & 3 & 1 & 0\\
1 & 2 & 0 & 1
\end{array}\right]
\begin{array}{c}
\text{substract row II}\\
\\
\end{array}\\
&\qquad\quad\Downarrow\\
&\left[\begin{array}{cc|cc}
1 & 1 & 1 & -1\\
1 & 2 & 0 & 1
\end{array}\right]
\begin{array}{c}
\\
\text{substract row I}
\end{array}\\
&\qquad\quad\Downarrow\\
&\left[\begin{array}{cc|cc}
1 & 1 & 1 & -1\\
0 & 1 & -1 & 2
\end{array}\right]
\begin{array}{c}
\text{substract row II}\\
\\
\end{array}\\
&\qquad\quad\Downarrow\\
&\left[\begin{array}{cc|cc}
{\color{Green}\mathbf{1}} & 0 & 2 & -3\\
0 & {\color{Green}\mathbf{1}} & -1 & 2
\end{array}\right]
\\
&\qquad\mathbf{I}_2\qquad\mathbf{A}_e^{-1}\\ \\
\mathbf{A}_e^{-1} =
&\left[\begin{array}{cc}
2 & -3\\
-1 & 2
\end{array}\right]
\end{align}](/wiki/robotics/images/math/5/9/5/595610169c9b8a5dbd3bec7d62a44795.png)
| Example: Gauß-Jordan-Algorithm for a 4-by-4 matrix
This example describes the computation of the inverse of the transform matrix |
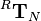that is introduced in the script on page 3-37 and used on the following pages.
![\begin{align}
\mathbf{A}_e =
&\left[\begin{array}{cccc}
1 & 2 & 0 & 0\\
3 & 0 & 1 & 1\\
0 & 1 & 0 & 0\\
0 & 0 & 2 & 1
\end{array}\right]\\ \\
(\mathbf{A}_e|\mathbf{I}_n) =
&\left[\begin{array}{cccc|cccc}
1 & 2 & 0 & 0 & 1 & 0 & 0 & 0\\
3 & 0 & 1 & 1 & 0 & 1 & 0 & 0\\
0 & 1 & 0 & 0 & 0 & 0 & 1 & 0\\
0 & 0 & 2 & 1 & 0 & 0 & 0 & 1
\end{array}\right]
\begin{array}{c}
\\
\updownarrow\text{interchange row II and row III}\\
\\
\end{array}\\
&\qquad\qquad\quad\quad\Downarrow\\
&\left[\begin{array}{cccc|cccc}
1 & 2 & 0 & 0 & 1 & 0 & 0 & 0\\
0 & 1 & 0 & 0 & 0 & 0 & 1 & 0\\
3 & 0 & 1 & 1 & 0 & 1 & 0 & 0\\
0 & 0 & 2 & 1 & 0 & 0 & 0 & 1
\end{array}\right]
\begin{array}{c}
\text{substract 2 times row II}\\
\\
\\
\\
\end{array}\\
&\qquad\qquad\quad\quad\Downarrow\\
&\left[\begin{array}{cccc|cccc}
1 & 0 & 0 & 0 & 1 & 0 & -2 & 0\\
0 & 1 & 0 & 0 & 0 & 0 & 1 & 0\\
3 & 0 & 1 & 1 & 0 & 1 & 0 & 0\\
0 & 0 & 2 & 1 & 0 & 0 & 0 & 1
\end{array}\right]
\begin{array}{c}
\\
\\
\text{substract 3 times row I}\\
\\
\end{array}\\
&\qquad\qquad\quad\quad\Downarrow\\
&\left[\begin{array}{cccc|cccc}
1 & 0 & 0 & 0 & 1 & 0 & -2 & 0\\
0 & 1 & 0 & 0 & 0 & 0 & 1 & 0\\
0 & 0 & 1 & 1 & -3 & 1 & 6 & 0\\
0 & 0 & 2 & 1 & 0 & 0 & 0 & 1
\end{array}\right]
\begin{array}{c}
\\
\\
\updownarrow\text{interchange row III and row IV}\\
\end{array}\\
&\qquad\qquad\quad\quad\Downarrow\\
&\left[\begin{array}{cccc|cccc}
1 & 0 & 0 & 0 & 1 & 0 & -2 & 0\\
0 & 1 & 0 & 0 & 0 & 0 & 1 & 0\\
0 & 0 & 2 & 1 & 0 & 0 & 0 & 1\\
0 & 0 & 1 & 1 & -3 & 1 & 6 & 0
\end{array}\right]
\begin{array}{c}
\\
\\
\text{substract row IV}\\
\\
\end{array}\\
&\qquad\qquad\quad\quad\Downarrow\\
&\left[\begin{array}{cccc|cccc}
1 & 0 & 0 & 0 & 1 & 0 & -2 & 0\\
0 & 1 & 0 & 0 & 0 & 0 & 1 & 0\\
0 & 0 & 1 & 0 & 3 & -1 & -6 & 1\\
0 & 0 & 1 & 1 & -3 & 1 & 6 & 0
\end{array}\right]
\begin{array}{c}
\\
\\
\\
\text{substract row III}\\
\end{array}\\
&\qquad\qquad\quad\quad\Downarrow\\
&\left[\begin{array}{cccc|cccc}
{\color{Green}\mathbf{1}} & 0 & 0 & 0 & 1 & 0 & -2 & 0\\
0 & {\color{Green}\mathbf{1}} & 0 & 0 & 0 & 0 & 1 & 0\\
0 & 0 & {\color{Green}\mathbf{1}} & 0 & 3 & -1 & -6 & 1\\
0 & 0 & 0 & {\color{Green}\mathbf{1}} & -6 & 2 & 12 & -1
\end{array}\right]\\
&\qquad\quad\mathbf{I}_n\qquad\qquad\qquad\mathbf{A}_e^{-1}\\ \\
\mathbf{A}_e^{-1} =
&\left[\begin{array}{cccc}
1 & 0 & -2 & 0\\
0 & 0 & 1 & 0\\
3 & -1 & -6 & 1\\
-6 & 2 & 12 & -1
\end{array}\right]
\end{align}](/wiki/robotics/images/math/b/2/5/b2511accef61ba621f855cc4cbd103f6.png)
