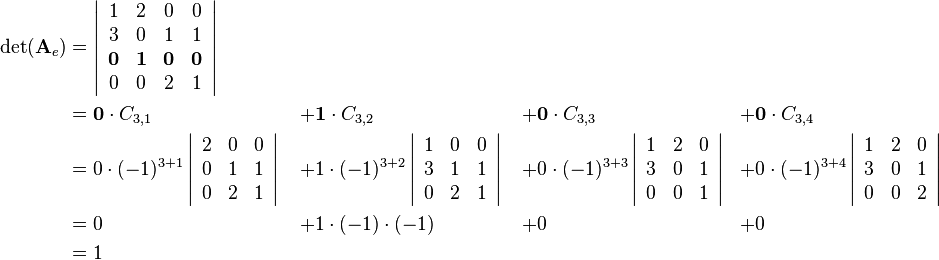Difference between revisions of "Determinant of a matrix"
| Line 2: | Line 2: | ||
The determinant can be computed for an n-by-n square matrix. In the context of matrices the determinant of a matrix is a special function that assigns a scalar value to the matrix. It is denoted with <math>\det(\mathbf{A})</math> or in matrix structure with vertical lines:<br/> | The determinant can be computed for an n-by-n square matrix. In the context of matrices the determinant of a matrix is a special function that assigns a scalar value to the matrix. It is denoted with <math>\det(\mathbf{A})</math> or in matrix structure with vertical lines:<br/> | ||
| − | :<math> | + | :<math>\begin{align} |
| − | \det(\mathbf{A})= | + | \det(\mathbf{A})&= |
\begin{array}{|ccc|} | \begin{array}{|ccc|} | ||
a_{11} & \dots & a_{1n}\\ | a_{11} & \dots & a_{1n}\\ | ||
\vdots & \ddots & \vdots\\ | \vdots & \ddots & \vdots\\ | ||
| − | a_{n1} & \dots & a_{nn} | + | a_{n1} & \dots & a_{nn} |
| − | \end{array} | + | \end{array} & |
| − | </math> | + | \end{align}</math> |
Considering a matrix as a linear system the determinant provides information about its solvability. If the determinant is nonzero the linear system is clearly solvable. This feature is also important for [[Matrix inversion|matrix inversion]]. | Considering a matrix as a linear system the determinant provides information about its solvability. If the determinant is nonzero the linear system is clearly solvable. This feature is also important for [[Matrix inversion|matrix inversion]]. | ||
Revision as of 10:54, 22 May 2014
| ← Back: Minors and cofactors | Overview: Matrices | Next: Matrix inversion → |
The determinant can be computed for an n-by-n square matrix. In the context of matrices the determinant of a matrix is a special function that assigns a scalar value to the matrix. It is denoted with 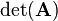 or in matrix structure with vertical lines:
or in matrix structure with vertical lines:
Considering a matrix as a linear system the determinant provides information about its solvability. If the determinant is nonzero the linear system is clearly solvable. This feature is also important for matrix inversion.
2-by-2 matrices
For a 2-by-2 matrix the determinant can easily computed as follows:
|
3-by-3 matrices
For 3-by-3 matrices there is a formula to compute the determinant using cramer's rule. The Khan Academy[1] provides a good video [2] where this formula is explained. Please watch the video for further information about the computation of the determinant of a 3-by-3 matrix.
4-by-4 matrices
One possibility to compute the determinant of a 4-by-4 matrix is a formula that uses the minors and cofactors of a matrix. First one row or column has to be choosen. The sum of the four corresponding values of the row or column multiplied by the related cofactors results in the determinant:

|
References
- ↑ https://www.khanacademy.org/ Khan Academy
- ↑ https://www.khanacademy.org/.../finding-the-determinant-of-a-3x3-matrix-method-1 Determinant of a 3-by-3 matrix
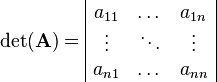
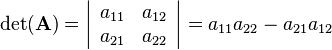
![\det
\left[\begin{array}{cc}
1 & 3\\
2 & 2
\end{array}\right] =
\left|\begin{array}{cc}
1 & 3\\
2 & 2
\end{array}\right|=
1\cdot 2-3\cdot 2=
2-6=-4](/wiki/robotics/images/math/f/a/e/faea73a114f85c32eb6c31664358eadc.png)
![\mathbf{A}_e =
\left[\begin{array}{cccc}
1 & 2 & 0 & 0\\
3 & 0 & 1 & 1\\
0 & 1 & 0 & 0\\
0 & 0 & 2 & 1
\end{array}\right]](/wiki/robotics/images/math/a/3/8/a386cb4eac26aca26ac89fd336061a0e.png)
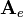 it is useful to choose row 3 because it contains three zero values as factors:
it is useful to choose row 3 because it contains three zero values as factors: