Difference between revisions of "Adjugate Formula"
From Robotics
(Created page with "The adjugate formula defines the inverse of an n-by-n square matrix <math>\mathbf{A}</math> as<br/><br/> <math>\mathbf{A}^{-1}=\frac{1}{\det(\mathbf{A})}\text{adj}(\mathbf{A})...") |
|||
| Line 5: | Line 5: | ||
\text{adj}(\mathbf{A})=\mathbf{C}(\mathbf{A})^T | \text{adj}(\mathbf{A})=\mathbf{C}(\mathbf{A})^T | ||
</math><br/><br/> | </math><br/><br/> | ||
| − | And the '''cofactor matrix''' <math>\mathbf{C}(\mathbf{A})</math> is just a matrix where each cell corresponds to the related cofactor:<br/><br/> | + | And the '''cofactor matrix''' <math>\mathbf{C}(\mathbf{A})</math> is just a matrix where each cell corresponds to the related [[Minors_and_cofactors|cofactor]]:<br/><br/> |
<math> | <math> | ||
\mathbf{C}(\mathbf{A})=\left[\begin{array}{cccc} | \mathbf{C}(\mathbf{A})=\left[\begin{array}{cccc} | ||
Revision as of 15:55, 9 May 2014
The adjugate formula defines the inverse of an n-by-n square matrix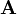 
as
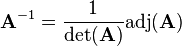
where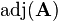 
is the so called adjugate matrix of 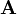. The adjugate matrix is the transposed of the cofactor matrix:
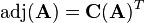
And the cofactor matrix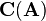 
is just a matrix where each cell corresponds to the related cofactor:
![\mathbf{C}(\mathbf{A})=\left[\begin{array}{cccc}
C_{1,1}(\mathbf{A}) & C_{1,2}(\mathbf{A}) & \cdots & C_{1,n}(\mathbf{A})\\
C_{2,1}(\mathbf{A}) & C_{2,2}(\mathbf{A}) & & C_{2,n}(\mathbf{A})\\
\vdots & & \ddots & \vdots\\
C_{n,1}(\mathbf{A}) & C_{n,2}(\mathbf{A}) & \cdots & C_{n,n}(\mathbf{A})
\end{array}\right]](/wiki/robotics/images/math/c/b/7/cb7505ec4a107c95fd31601fac888472.png)
So to determine the inverse of an n-by-n square matrix you have to compute the n square cofactors, then transpose the resulting cofactor matrix and divide all the values by the determinant.
![\begin{align}
\mathbf{C}(\mathbf{A}_e)&=
\left[\begin{array}{cccc}
1 & 0 & 3 & -6\\
0 & 0 & -1 & 2\\
-2 & 1 & -6 & 12\\
0 & 0 & 1 & -1
\end{array}\right]\\ \\
\mathbf{C}(\mathbf{A}_e)^T&=
\left[\begin{array}{cccc}
1 & 0 & -2 & 0\\
0 & 0 & 1 & 0\\
3 & -1 & -6 & 1\\
-6 & 2 & 12 & -1
\end{array}\right]=\text{adj}(\mathbf{A}_e)\\ \\
\mathbf{A}_e^{-1}&=\frac{1}{\det(\mathbf{A}_e)}\text{adj}(\mathbf{A}_e)
=\frac{1}{1}
\left[\begin{array}{cccc}
1 & 0 & -2 & 0\\
0 & 0 & 1 & 0\\
3 & -1 & -6 & 1\\
-6 & 2 & 12 & -1
\end{array}\right]
=
\left[\begin{array}{cccc}
1 & 0 & -2 & 0\\
0 & 0 & 1 & 0\\
3 & -1 & -6 & 1\\
-6 & 2 & 12 & -1
\end{array}\right]
\end{align}](/wiki/robotics/images/math/0/1/9/0199318a1f83c5689378feb6507cc250.png)
