Difference between revisions of "A-matrices"
From Robotics
| Line 1: | Line 1: | ||
{{Navigation|before=[[Denavit-Hartenberg parameters]]|overview=[[Denavit-Hartenberg Convention]]|next=[[Typical link examples]]}} | {{Navigation|before=[[Denavit-Hartenberg parameters]]|overview=[[Denavit-Hartenberg Convention]]|next=[[Typical link examples]]}} | ||
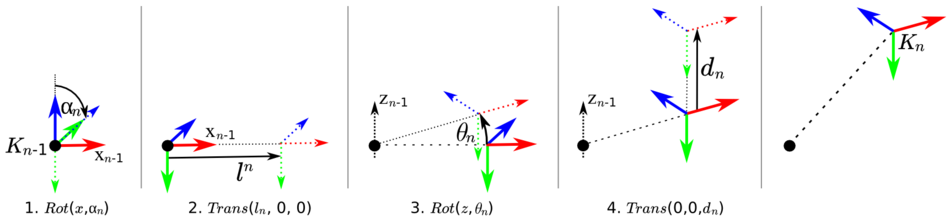
| − | In the previous articles, it was described how the transformation | + | The A-matrices describe the precise transformation between each two successive manipulator links. In the previous articles, it was described how the transformation can be described using [[Assigning coordinate frames|local coordinate frames]] and the 4 [[Denavit-Hartenberg parameters]]. The parameters describe 2 translational and 2 rotational degrees of freedom, which correspond to 4 transformations, that are applied successively to transform [[Assigning coordinate frames|coordinate frame]] <math>K_n</math> with respect to frame <math>K_{n-1}</math> like shown below. |
[[File:dh-params-steps.png|center|950px]] | [[File:dh-params-steps.png|center|950px]] | ||
| − | |||
[[File:amatrices.png|right|450px]] | [[File:amatrices.png|right|450px]] | ||
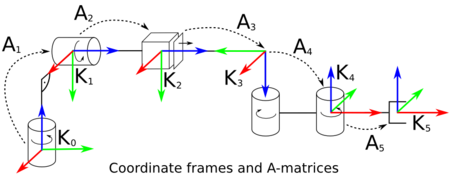
| − | + | The A-matrices now are used to combine the 4 successive transformations of the [[Denavit-Hartenberg parameters]] in one matrix. According to the figure above and following the rules for [[Combinations of transformations|combinations of transformations]], the combined A-matrix is determined as follows: | |
| + | :<math> | ||
| + | \begin{align} | ||
| + | A_n | ||
| + | &= | ||
| + | \mathbf{Trans}(0,0,d_n)\mathbf{Rot}(z,\theta_n)\mathbf{Trans}(l_n,0,0)\mathbf{Rot}(x, \alpha_n) \\ | ||
| + | &= | ||
| + | \left[\begin{array}{cccc} | ||
| + | 1 & 0 & 0 & 0 \\ | ||
| + | 0 & 1 & 0 & 0 \\ | ||
| + | 0 & 0 & 1 & d_n \\ | ||
| + | 0 & 0 & 0 & 1 | ||
| + | \end{array}\right] | ||
| + | \left[\begin{array}{cccc} | ||
| + | \cos{\theta_n} & -\sin{\theta_n} & 0 & 0 \\ | ||
| + | \sin{\theta_n} & \cos{\theta_n} & 0 & 0 \\ | ||
| + | 0 & 0 & 1 & d \\ | ||
| + | 0 & 0 & 0 & 1 | ||
| + | \end{array}\right] | ||
| + | \left[\begin{array}{cccc} | ||
| + | 1 & 0 & 0 & l_n \\ | ||
| + | 0 & 1 & 0 & 0 \\ | ||
| + | 0 & 0 & 1 & 0 \\ | ||
| + | 0 & 0 & 0 & 1 | ||
| + | \end{array}\right] | ||
| + | \left[\begin{array}{cccc} | ||
| + | 1 & 0 & 0 & 0 \\ | ||
| + | 0 & \cos{\alpha_n} & -\sin{\alpha_n} & 0 \\ | ||
| + | 0 & \sin{\alpha_n} & \cos{\alpha_n} & 0 \\ | ||
| + | 0 & 0 & 1 & d \\ | ||
| + | 0 & 0 & 0 & 1 | ||
| + | \end{array}\right] | ||
| + | \end{align} | ||
| + | </math> | ||
[[Category:Article]] | [[Category:Article]] | ||
[[Category:Denavit-Hartenberg]] | [[Category:Denavit-Hartenberg]] | ||
Revision as of 11:54, 17 November 2015
| ← Back: Denavit-Hartenberg parameters | Overview: Denavit-Hartenberg Convention | Next: Typical link examples → |
The A-matrices describe the precise transformation between each two successive manipulator links. In the previous articles, it was described how the transformation can be described using local coordinate frames and the 4 Denavit-Hartenberg parameters. The parameters describe 2 translational and 2 rotational degrees of freedom, which correspond to 4 transformations, that are applied successively to transform coordinate frame 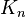 with respect to frame
with respect to frame 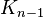 like shown below.
like shown below.
The A-matrices now are used to combine the 4 successive transformations of the Denavit-Hartenberg parameters in one matrix. According to the figure above and following the rules for combinations of transformations, the combined A-matrix is determined as follows:
![\begin{align}
A_n
&=
\mathbf{Trans}(0,0,d_n)\mathbf{Rot}(z,\theta_n)\mathbf{Trans}(l_n,0,0)\mathbf{Rot}(x, \alpha_n) \\
&=
\left[\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & d_n \\
0 & 0 & 0 & 1
\end{array}\right]
\left[\begin{array}{cccc}
\cos{\theta_n} & -\sin{\theta_n} & 0 & 0 \\
\sin{\theta_n} & \cos{\theta_n} & 0 & 0 \\
0 & 0 & 1 & d \\
0 & 0 & 0 & 1
\end{array}\right]
\left[\begin{array}{cccc}
1 & 0 & 0 & l_n \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{array}\right]
\left[\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & \cos{\alpha_n} & -\sin{\alpha_n} & 0 \\
0 & \sin{\alpha_n} & \cos{\alpha_n} & 0 \\
0 & 0 & 1 & d \\
0 & 0 & 0 & 1
\end{array}\right]
\end{align}](/wiki/robotics/images/math/3/e/6/3e61a1617e11087d1efef73dec332751.png)