A-matrices
| ← Back: Denavit-Hartenberg parameters | Overview: Denavit-Hartenberg Convention | Next: Typical link examples → |
The A-matrices describe the precise transformation between each two successive manipulator links. In the previous articles, it was described how the transformation can be described using local coordinate frames and the 4 Denavit-Hartenberg parameters. The parameters describe 2 translational and 2 rotational degrees of freedom, which correspond to 4 transformations, that are applied successively to transform coordinate frame 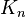 with respect to frame
with respect to frame 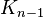 like shown below.
like shown below.
The A-matrices now are used to combine the 4 successive transformations of the Denavit-Hartenberg parameters in one matrix. According to the figure above and following the rules for combinations of transformations, the combined A-matrix is determined as follows:
So the A-matrix for link 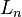 can just be computed by setting in the parameters
can just be computed by setting in the parameters 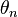 ,
, 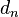 ,
, 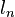 and
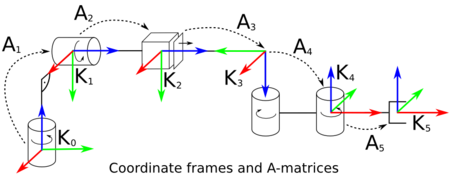
and 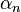 determined before. As shown in the figure on the right,
determined before. As shown in the figure on the right, 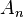 then describes the transformation between the coordinate frames
then describes the transformation between the coordinate frames 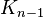 at the beginning and
at the beginning and 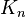 at the end of link
at the end of link 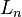 including the static transformation as well as the translation or rotation caused by the joint
including the static transformation as well as the translation or rotation caused by the joint 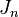 .
.
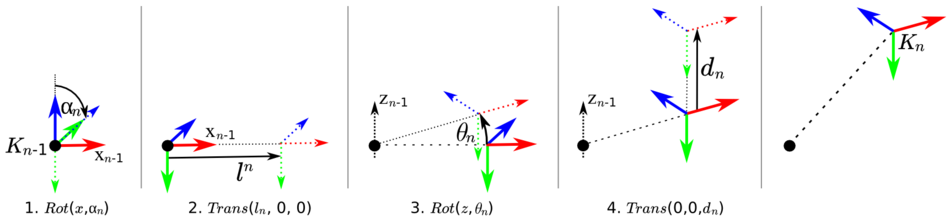
![\begin{align}
A_n
&=
\mathbf{Trans}(0,0,d_n)\mathbf{Rot}(z,\theta_n)\mathbf{Trans}(l_n,0,0)\mathbf{Rot}(x, \alpha_n) \\
&=
\left[\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & d_n \\
0 & 0 & 0 & 1
\end{array}\right]
\left[\begin{array}{cccc}
\cos{\theta_n} & -\sin{\theta_n} & 0 & 0 \\
\sin{\theta_n} & \cos{\theta_n} & 0 & 0 \\
0 & 0 & 1 & d \\
0 & 0 & 0 & 1
\end{array}\right]
\left[\begin{array}{cccc}
1 & 0 & 0 & l_n \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{array}\right]
\left[\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & \cos{\alpha_n} & -\sin{\alpha_n} & 0 \\
0 & \sin{\alpha_n} & \cos{\alpha_n} & 0 \\
0 & 0 & 0 & 1
\end{array}\right] \\
&=
\left[\begin{array}{cccc}
\cos{\theta_n} & -\sin{\theta_n}\cos{\alpha_n} & \sin{\theta_n}\sin{\alpha_n} & l\cos{\theta_n} \\
\sin{\theta_n} & \cos{\theta_n}\cos{\alpha_n} & -\cos{\theta_n}\sin{\alpha_n} & l\sin{\theta_n} \\
0 & \sin{\alpha_n} & \cos{\alpha_n} & d \\
0 & 0 & 0 & 1
\end{array}\right]
\end{align}](/wiki/robotics/images/math/6/6/1/6614ed6d8b773814736d932d2f5662be.png)