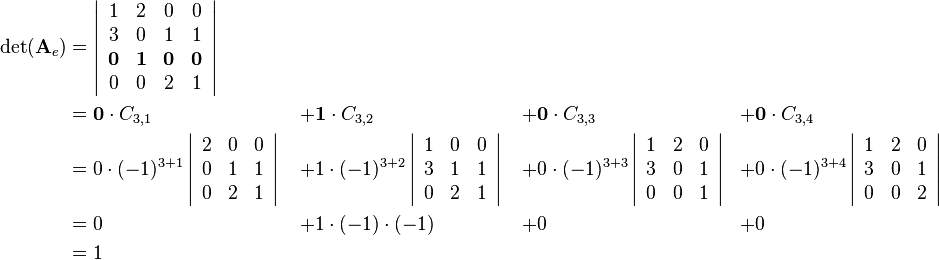Determinant of a matrix
| ← Back: Minors and cofactors | Overview: Matrices | Next: Matrix inversion → |
In the context of matrices the determinant of a matrix is a special function For 3-by-3 and smaller matrices there are simple formulas to compute the determinant. Useful to compute the determinant of larger matrices are the minors and cofactors which are explained in the first subarticle. Based on these an example formula to compute the determinant of a 4-by-4 matrix is presented afterwards.
This article describes a formula to compute the determinant of a 4-by-4 matrix using minors and cofactors of a matrix.
To compute the determinant of matrix 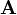 first one row or column is choosen. The sum of the four corresponding values of the row or column multiplied by the related cofactors results in the determinant:
first one row or column is choosen. The sum of the four corresponding values of the row or column multiplied by the related cofactors results in the determinant:

|
![\mathbf{A}_e =
\left[\begin{array}{cccc}
1 & 2 & 0 & 0\\
3 & 0 & 1 & 1\\
0 & 1 & 0 & 0\\
0 & 0 & 2 & 1
\end{array}\right]](/wiki/robotics/images/math/a/3/8/a386cb4eac26aca26ac89fd336061a0e.png)
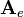 it is useful to choose row 3 because it contains three zero values as factors:
it is useful to choose row 3 because it contains three zero values as factors: