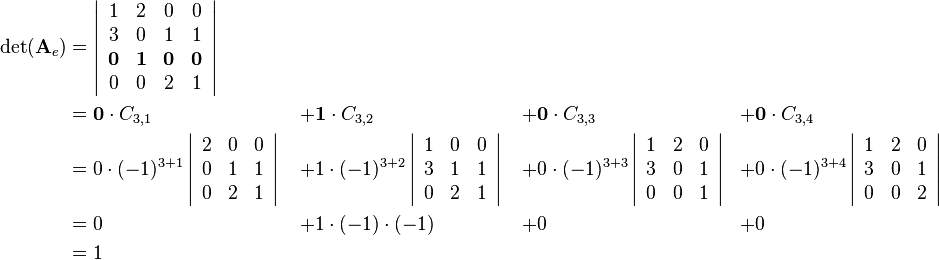Difference between revisions of "Determinant of a matrix"

From Robotics
Jump to: navigation, search
Line 44: Line 44:
 
<br/>
 
<br/>
  
−
For 3-by-3 and smaller matrices there are simple formulas to compute the determinant. Useful to compute the determinant of larger matrices are the minors and cofactors which are explained in the first subarticle. Based on these an example formula to compute the determinant of a 4-by-4 matrix is presented afterwards.
+
===3-by-3 matrices===
  
−
This article describes a formula to compute the determinant of a 4-by-4 matrix using [[Minors_and_cofactors|minors and cofactors]] of a matrix.<br/>
+
For 3-by-3 matrices there is a formula to compute the determinant using cramer's rule. The Khan Academy provides a good video where this formula is explained. Please watch the video for further information about the computation of the determinant of a 3-by-3 matrix.
  
−
To compute the determinant of matrix <math>\mathbf{A}</math> first one row or column is choosen. The sum of the four corresponding values of the row or column multiplied by the related cofactors results in the determinant:<br/><br/>
+
===4-by-4 matrices===
 +
 
 +
One possibility to compute the determinant of a 4-by-4 matrix is a formula that uses the [[Minors_and_cofactors|minors and cofactors]] of a matrix. First one row or column has to be choosen. The sum of the four corresponding values of the row or column multiplied by the related cofactors results in the determinant:<br/><br/>
  
 
<math>
 
<math>

Revision as of 15:12, 19 May 2014

← Back: Minors and cofactors Overview: Matrices Next: Matrix inversion →

The determinant can be computed for an n-by-n square matrix. In the context of matrices the determinant of a matrix is a special function that assigns a scalar value to the matrix. It is denoted with 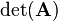\det(\mathbf{A}) or in matrix structure with vertical lines:

\det(\mathbf{A})= \left|\begin{array}{ccc} a_{11} & \dots & a_{1n}\\ \vdots & \ddots & \vdots\\ a_{n1} & \dots & a_{nn} \end{array}\right|

Considering a matrix as a linear system the determinant provides information about its solvability. If the determinant is nonzero the linear system is clearly solvable. This feature is also important for matrix inversion.

2-by-2 matrices

For a 2-by-2 matrix the determinant can easily computed as follows:

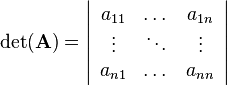
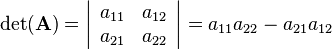
\det(\mathbf{A})= \left|\begin{array}{cc} a_{11} & a_{12}\\ a_{21} & a_{22} \end{array}\right|=a_{11}a_{22}-a_{21}a_{12}


Example: Determinant of a 2-by-2 matrix


\det \left[\begin{array}{cc} 1 & 3\\ 2 & 2 \end{array}\right] = \left|\begin{array}{cc} 1 & 3\\ 2 & 2 \end{array}\right|= 1\cdot 2-3\cdot 2= 2-6=-4


3-by-3 matrices

For 3-by-3 matrices there is a formula to compute the determinant using cramer's rule. The Khan Academy provides a good video where this formula is explained. Please watch the video for further information about the computation of the determinant of a 3-by-3 matrix.

4-by-4 matrices

One possibility to compute the determinant of a 4-by-4 matrix is a formula that uses the minors and cofactors of a matrix. First one row or column has to be choosen. The sum of the four corresponding values of the row or column multiplied by the related cofactors results in the determinant:

\det(\mathbf{A})=\sum_{(i,j) \isin \text{ one row or column}}{a_{i,j}C_{i,j}}

Example: determinant of a 4-by-4 matrix


\mathbf{A}_e = \left[\begin{array}{cccc} 1 & 2 & 0 & 0\\ 3 & 0 & 1 & 1\\ 0 & 1 & 0 & 0\\ 0 & 0 & 2 & 1 \end{array}\right]

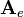For matrix \mathbf{A}_e it is useful to choose row 3 because it contains three zero values as factors:

\begin{align} \det(\mathbf{A}_e)&= \left|\begin{array}{cccc} 1 & 2 & 0 & 0\\ 3 & 0 & 1 & 1\\ \mathbf{0} & \mathbf{1} & \mathbf{0} & \mathbf{0}\\ 0 & 0 & 2 & 1 \end{array}\right| & \quad & \quad & \quad\\ &= \mathbf{0}\cdot C_{3,1}&+&\mathbf{1}\cdot C_{3,2}&+&\mathbf{0}\cdot C_{3,3}&+&\mathbf{0}\cdot C_{3,4}\\ &= 0\cdot(-1)^{3+1} \left|\begin{array}{ccc} 2 & 0 & 0\\ 0 & 1 & 1\\ 0 & 2 & 1 \end{array}\right| &+&1\cdot(-1)^{3+2} \left|\begin{array}{ccc} 1 & 0 & 0\\ 3 & 1 & 1\\ 0 & 2 & 1 \end{array}\right| &+&0\cdot(-1)^{3+3} \left|\begin{array}{ccc} 1 & 2 & 0\\ 3 & 0 & 1\\ 0 & 0 & 1 \end{array}\right| &+&0\cdot(-1)^{3+4} \left|\begin{array}{ccc} 1 & 2 & 0\\ 3 & 0 & 1\\ 0 & 0 & 2 \end{array}\right|\\ &= 0&+&1\cdot(-1)\cdot(-1)&+&0&+&0\\ &= 1&\quad&\quad&\quad \end{align}

Retrieved from "https://getwww.uni-paderborn.de/wiki/robotics/index.php?title=Determinant_of_a_matrix&oldid=360"