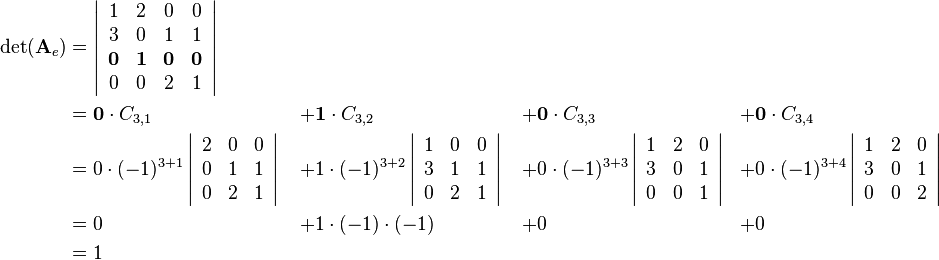Difference between revisions of "Determinant of a matrix"
| Line 5: | Line 5: | ||
\det(\mathbf{A})= | \det(\mathbf{A})= | ||
\left|\begin{array}{ccc} | \left|\begin{array}{ccc} | ||
| − | a_{11} & | + | a_{11} & \dots & a_{1n}\\ |
| − | \ | + | \vdots & \ddots & \vdots\\ |
| + | a_{n1} & \dots & a_{nn} | ||
| + | \end{array}\right| | ||
</math> | </math> | ||
Revision as of 14:57, 19 May 2014
| ← Back: Minors and cofactors | Overview: Matrices | Next: Matrix inversion → |
In the context of matrices the determinant of a matrix is a special function that assigns a scalar value to the matrix. It is denoted with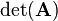 
or in matrix structure with vertical lines:
Considering a matrix as a linear system the determinant provides information about its solvability. If the determinant is nonzero the linear system is clearly solvable. This feature is also important for matrix inversion.
,
For 3-by-3 and smaller matrices there are simple formulas to compute the determinant. Useful to compute the determinant of larger matrices are the minors and cofactors which are explained in the first subarticle. Based on these an example formula to compute the determinant of a 4-by-4 matrix is presented afterwards.
This article describes a formula to compute the determinant of a 4-by-4 matrix using minors and cofactors of a matrix.
To compute the determinant of matrix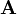 
first one row or column is choosen. The sum of the four corresponding values of the row or column multiplied by the related cofactors results in the determinant:
 Example: determinant of a 4-by-4 matrix
|
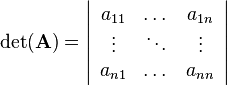
![\mathbf{A}_e =
\left[\begin{array}{cccc}
1 & 2 & 0 & 0\\
3 & 0 & 1 & 1\\
0 & 1 & 0 & 0\\
0 & 0 & 2 & 1
\end{array}\right]](/wiki/robotics/images/math/a/3/8/a386cb4eac26aca26ac89fd336061a0e.png)
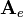it is useful to choose row 3 because it contains three zero values as factors:
