Difference between revisions of "Matrices"
From Robotics
| Line 10: | Line 10: | ||
\end{array}\right] | \end{array}\right] | ||
</math> | </math> | ||
| − | Individual colums and rows are often denoted as column vectors and row vectors. For the example matrix the column vectors are | + | Individual colums and rows are often denoted as column vectors and row vectors. For the example matrix <math>\mathbf{A}</math> the column vectors are |
:<math> | :<math> | ||
\left[ | \left[ | ||
Revision as of 15:40, 15 May 2014
This article deals with some fundamental matrix features and the basic arithmetic operations.
Matrices can have arbitrary dimensions. A matrix with m rows and n colums is denoted as an m-by-n matrix. In the context of robotics mainly 3-by-3 or 4-by-4 matrices are used. An example of a 3-by-3 matrix is:
![\mathbf{A}=\left[
\begin{array}{ccc}
a_{11} & a_{12} & a_{13}\\
a_{21} & a_{22} & a_{23}\\
a_{31} & a_{32} & a_{33}
\end{array}\right]](/wiki/robotics/images/math/2/1/5/215a86cdc852123b36edb8d3747065f5.png)
Individual colums and rows are often denoted as column vectors and row vectors. For the example matrix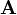 
the column vectors are
![\left[
\begin{array}{c}
a_{11}\\
a_{21}\\
a_{31}
\end{array}\right],
\left[
\begin{array}{c}
a_{12}\\
a_{22}\\
a_{32}
\end{array}\right],\text{and }
\left[
\begin{array}{c}
a_{13}\\
a_{23}\\
a_{33}
\end{array}\right]](/wiki/robotics/images/math/2/1/9/2198ba7778b8f7508d3ac527dac237a3.png)
and the row vectors are
![\left[
\begin{array}{ccc}
a_{11} & a_{12} & a_{13}
\end{array}\right],
\left[
\begin{array}{ccc}
a_{21} & a_{22} & a_{23}
\end{array}\right],\text{and }
\left[
\begin{array}{ccc}
a_{31} & a_{32} & a_{33}
\end{array}\right]](/wiki/robotics/images/math/8/5/f/85f9c7ad76b41e74aaf41e01452797b1.png)
In the following subarticles some basic arithmetic operations for matrices are described.
