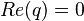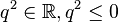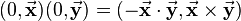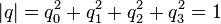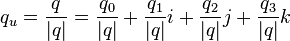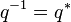Difference between revisions of "Pure and unit quaternions"

From Robotics
Jump to: navigation, search
 
(10 intermediate revisions by the same user not shown)
Line 1: Line 1:
−
{{Navigation|before=[[Definition of a quaternion]]|overview=[[Quaternions]]|next=[[Rotations with quaternions]]}}
+
{{Navigation|before=[[Basic properties of quaternions]]|overview=[[Quaternions]]|next=[[Addition of quaternions]]}}
 +
__NOTOC__
 +
===Pure quaternion===
 +
A quaternion whose vector part is zero equals a real number corresponding to the scalar part.
  
−
For these imaginary units, the following rules hold:
+
A quaternion whose scalar part is zero, is called a pure quaternion:
 
:<math>
 
:<math>
−
\begin{align}
+
Re(q) = 0
−
i^2 &= j^2 = k^2 = ijk = -1 \\
 
−
ij &= -ji = k \\
 
−
jk &= -kj = i \\
 
−
ki &= -ik = j
 
−
\end{align}
 
 
</math>
 
</math>
 +
 +
The square of a pure quaternion is always real and not positive:
 +
:<math>
 +
q^2 \in \R, q^2\le 0
 +
</math>
 +
 +
Multiplication of pure quaternions leads to the following simplified equation (for the general equation see chapter [[Multiplication of quaternions]]):
 +
:<math>
 +
(0,\vec{\mathbf{x}})(0,\vec{\mathbf{y}})=(-\vec{\mathbf{x}}\cdot\vec{\mathbf{y}},\vec{\mathbf{x}}\times\vec{\mathbf{y}})
 +
</math>
 +
 +
===Unit quaternion===
 +
A unit quaternion, also called normalized quaternion, has a magnitude of 1:
 +
:<math>
 +
|q| = q_0^2 + q_1^2 + q_2^2 + q_3^2 = 1
 +
</math>
 +
A unit quaternion can be created from any quaternion by dividing it and so the four components by its norm:
 +
:<math>
 +
q_u = \frac{q}{|q|} = \frac{q_0}{|q|} + \frac{q_1}{|q|}i + \frac{q_2}{|q|}j + \frac{q_3}{|q|}k
 +
</math>
 +
The product of two unit quaternions and the inverse of a unit quaternion are again unit quaternions.
 +
 +
If <math>q</math> is a unit quaternion, its [[Basic properties of quaternions|inverse]] equals its [[Basic properties of quaternions|conjugate]]:
 +
:<math>
 +
q^{-1}=q^*
 +
</math>
 +
 +
[[Category:Article]]
 +
[[Category:Quaternion]]

Latest revision as of 15:59, 8 September 2015

← Back: Basic properties of quaternions Overview: Quaternions Next: Addition of quaternions →

Pure quaternion

A quaternion whose vector part is zero equals a real number corresponding to the scalar part.

A quaternion whose scalar part is zero, is called a pure quaternion:

Re(q) = 0

The square of a pure quaternion is always real and not positive:

q^2 \in \R, q^2\le 0

Multiplication of pure quaternions leads to the following simplified equation (for the general equation see chapter Multiplication of quaternions):

(0,\vec{\mathbf{x}})(0,\vec{\mathbf{y}})=(-\vec{\mathbf{x}}\cdot\vec{\mathbf{y}},\vec{\mathbf{x}}\times\vec{\mathbf{y}})

Unit quaternion

A unit quaternion, also called normalized quaternion, has a magnitude of 1:

|q| = q_0^2 + q_1^2 + q_2^2 + q_3^2 = 1

A unit quaternion can be created from any quaternion by dividing it and so the four components by its norm:

q_u = \frac{q}{|q|} = \frac{q_0}{|q|} + \frac{q_1}{|q|}i + \frac{q_2}{|q|}j + \frac{q_3}{|q|}k

The product of two unit quaternions and the inverse of a unit quaternion are again unit quaternions.

If 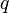q is a unit quaternion, its inverse equals its conjugate:

q^{-1}=q^*
Retrieved from "https://getwww.uni-paderborn.de/wiki/robotics/index.php?title=Pure_and_unit_quaternions&oldid=1601"