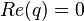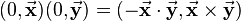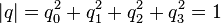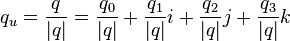Pure and unit quaternions

← Back: Basic properties of quaternions

Overview: Quaternions

Next: Addition of quaternions →

Pure quaternion

A quaternion whose vector part is zero equals a real number corresponding to the scalar part.

A quaternion whose scalar part is zero, is called a pure quaternion:

$Re(q) = 0$

The square of a pure quaternion is always real and not positive:

$q^2 \in \R, q^2\le 0$

Multiplication of pure quaternions leads to the following simplified equation (for the general equation see chapter Multiplication of quaternions):

$(0,\vec{\mathbf{x}})(0,\vec{\mathbf{y}})=(-\vec{\mathbf{x}}\cdot\vec{\mathbf{y}},\vec{\mathbf{x}}\times\vec{\mathbf{y}})$

Unit quaternion

A unit quaternion, also called normalized quaternion, has a magnitude of 1:

$|q| = q_0^2 + q_1^2 + q_2^2 + q_3^2 = 1$

A unit quaternion can be created from any quaternion by dividing it and so the four components by its norm:

$q_u = \frac{q}{|q|} = \frac{q_0}{|q|} + \frac{q_1}{|q|}i + \frac{q_2}{|q|}j + \frac{q_3}{|q|}k$

The product of two unit quaternions and the inverse of a unit quaternion are again unit quaternions.

If 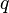$q$ is a unit quaternion, its inverse equals its conjugate:

$q^{-1}=q^*$