Wegelemente

Wegelemente

Betrachtet man in der Abbildung das Wegelement 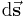$\mathrm{d}\vec{\mathbf{s}}$, so fällt auf, dass es in beliebige Richtungen zeigt (hä? woran soll das hier auffallen?), ebenso wie auch die Kontur im Durchflutungssatz eine beliebige (nein, sie muss zumindest geschlossen sein, also isrt sie nicht beliebig) Form annehmen kann. Wichtig ist hierbei, dass das Wegelement 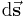$\mathrm{d}\vec{\mathbf{s}}$ als infinitesimales Wegstück aufgefasst werden soll. Es ist also ein sehr kleines Wegstück, so klein, dass die Krümmung des einzelnen Wegstücks vernachlässigbar wird.

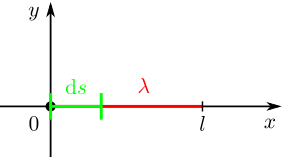
In den nebenstehenden Abbildungen (nebenstehend sind keine Abbildungen) sind zwei beispielhafte Verläufe einer Linienladung dargestellt. Im ersten Fall verläuft die Linienladung nur entlang der x-Achse. Das Wegelement kann hier also mit dem Differential 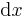$\mathrm{d}x$ dargestellt (wirklich dargestellt?) werden, da die zu integrierenden Funktion 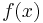$f(x)$ nur von x abhängt.

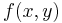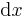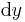Ist jedoch der Kurvenverlauf aus der zweiten Abbildung gegeben, ist die Funktion von x und y abhängig $f(x,y)$. Nun kann man nicht einfach nach $\mathrm{d}x$ und $\mathrm{d}y$ integrieren, weil so eine Fläche aufgespannt wird und man so ein Flächenelement 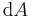$\mathrm{d}A$ erhält (Argumentation des letzten Satzes unschlüssig). Da hier ein Kreisbogen betrachtet wird, bietet sich die Verwendung von Polarkoordinaten, da so der Kreisbogen nur noch von einner Koordinaten $\varphi$ abhängt (1. Du sprechen Deutsch? 2. "Der Kreisbogen" ist doch Quatsch. Ist die LÄNGE DES KREISBOGENS gemeint?).

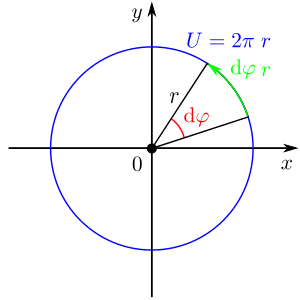
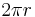Es muss darauf geachtet werden, dass vor allem bei den gekrümmten orthogonalen Koordinaten oft Korrekturfaktoren (Man weiß doch gar nicht, was Korrekturfaktoren sein sollen!) bei infinitesimalen Elementen zu berücksichtigen sind. Hier ist die Koordinate $\varphi$ auch vom Radius r abhängig. Dies entspricht einer Umfangsberechnung des Kreises. Der Kreis hat einen Gesamtumfang von $2\pi r$. Betrachtet man ein kleines Teilstück des Kreises folgt: 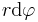$r\mathrm{d}\varphi$ (In Grafik untereinander darstellen).

In dieser Vorlesung werden nur einfache Verläufe entlang der Koordinatenachsen uns bekannter Koordinatensysteme verwendet (stimmt nicht!!!). Für kompliziertere Verläufe gibt es (besser: existieren) mathematische Hilfsmittel, auf die hier aber nicht näher eingegangen werden soll (wird!). 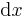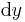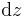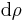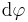Es werden hauptsächlich für Wegelemente in den kartesischen Koordinaten $\mathrm{d}x$,$\mathrm{d}y$ oder $\mathrm{d}z$, in den Zylinderkoordinaten $\mathrm{d}\rho$ oder $\mathrm{d}\varphi$ und in den Kugelkoordinaten 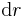$\mathrm{d}r$ verwendet (Du sprechen Deutsch?).