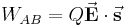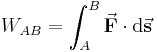Skalarprodukt: Unterschied zwischen den Versionen
| Zeile 51: | Zeile 51: | ||
W_{AB} = \int_{A}^{B} \vec{\textbf{F}} \cdot \mathrm{d}\vec{\textbf{s}} | W_{AB} = \int_{A}^{B} \vec{\textbf{F}} \cdot \mathrm{d}\vec{\textbf{s}} | ||
</math> | </math> | ||
| + | |||
| + | [[Datei:Elektrische_Arbeit.png|400px]] | ||
| + | |||
}} | }} | ||
Version vom 6. Februar 2012, 20:56 Uhr
Bei der Multiplikation zweier Vektoren handelt es sich entweder um das Vektorprodukt (auch Kreuzprodukt genannt) oder aber um das Skalarprodukt. Das Skalarprodukt liefert als Ergebnis ein Skalar, das Vektorprodukt hingegen liefert als Ergebnis wieder einen Vektor. Betrachtet man zwei Vektoren  und
und  , so ist das zugehörige Skalarprodukt wie folgt definiert:
, so ist das zugehörige Skalarprodukt wie folgt definiert:
Dabei bezeichnet 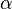 den Winkel, der von den beiden Vektoren eingeschlossen wird und Werte zwischen
den Winkel, der von den beiden Vektoren eingeschlossen wird und Werte zwischen 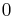 und
und 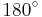 annehmen kann (siehe Abbildung). Der Einfachheit halber lässt man den Punkt zur Kennzeichnung des Skalarprodukts häufig weg, da bei der Multiplikation zweier Vektoren nur das Skalarprodukt und das Vektorprodukt in Frage kommen und letzteres ohnehin durch ein Kreuz (also zum Beispiel
annehmen kann (siehe Abbildung). Der Einfachheit halber lässt man den Punkt zur Kennzeichnung des Skalarprodukts häufig weg, da bei der Multiplikation zweier Vektoren nur das Skalarprodukt und das Vektorprodukt in Frage kommen und letzteres ohnehin durch ein Kreuz (also zum Beispiel 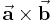 ) gekennzeichnet wird.
) gekennzeichnet wird.
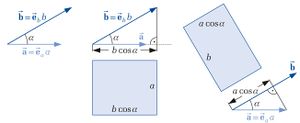
Betrachtet man nun die rechte Seite der oben angegebenen Beziehung zur Bestimmung des Skalarprodukts und die zugehörige Abbildung, so lässt sich der folgende Zusammenhang feststellen: Projiziert man den Vektor  auf die Richtung des Vektors
auf die Richtung des Vektors  , so erhält man hierbei gerade die Strecke
, so erhält man hierbei gerade die Strecke 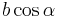 . Daraus folgt, dass das Ergebnis des Skalarprodukts als Flächeninhalt eines Rechtecks mit den Seitenlängen
. Daraus folgt, dass das Ergebnis des Skalarprodukts als Flächeninhalt eines Rechtecks mit den Seitenlängen 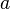 und
und 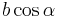 aufgefasst werden kann. Die Projektion kann auch in umgekehrter Reihenfolge (Projektion des Vektors
aufgefasst werden kann. Die Projektion kann auch in umgekehrter Reihenfolge (Projektion des Vektors  auf die Richtung des Vektors
auf die Richtung des Vektors  ) ausgeführt werden, so dass man die Strecke
) ausgeführt werden, so dass man die Strecke 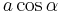 erhält. Die Multiplikation dieses Terms mit
erhält. Die Multiplikation dieses Terms mit 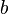 führt zu einem Rechteck mit identischem Flächeninhalt aber einem anderen Seitenverhältnis (siehe Abbildung).
führt zu einem Rechteck mit identischem Flächeninhalt aber einem anderen Seitenverhältnis (siehe Abbildung).
Eine weitere Möglichkeit zur Bestimmung des Skalarprodukts ist dadurch gegeben, dass man zunächst die korrespondierenden Komponenten multipliziert und anschließend aufsummiert:
Ganz allgemein - zum Beispiel wenn man es nicht mit Vektoren aus dem kartesischen Koordinatensystem zu tun hat - lässt sich das Skalarprodukt wie folgt bestimmen:
Anhand der beschriebenen Zusammenhänge zeigt sich, dass das Skalarprodukt dem Kommutativgesetz genügt. Somit gilt:
Weiterhin ergeben sich einige Sonderfälle, die im technischen Kontext häufig zu Vereinfachungen führen:
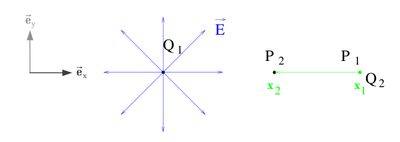
Ein häufiger Anwendungsfall des Skalarprodukts ergibt sich bei dem Begriff der Arbeit. Bewegt man beispielsweise eine Punktladung Bei der Verschiebung der Ladung muss die Coulomb-Kraft Allgemein, also wenn die elektrische Feldstärke nicht homogen und der Weg der Verschiebung keine gerade Strecke ist, gilt: |
Multimediale Lehrmaterialien
|
http://ksbg.educanet2.ch/fgmathematik1/kap_3_2/exp_3_2.html Applet: Skalarprodukt zweier Vektoren http://www.mathresource.iitb.ac.in/linear%20algebra/example7.1/index.html Applet: Skalarprodukt zweier Vektoren (engl.) http://www.cs.brown.edu/exploratories/freeSoftware/repository/edu/brown/cs/exploratories/applets/dotProduct/dot_product_java_browser.html Applet: Skalarprodukt zweier Vektoren http://www.mathresource.iitb.ac.in/linear%20algebra/example7.2/index.html Applet: Skalarprodukt zweier Vektoren mit der eingeschlossenen Fläche http://demonstrations.wolfram.com/DotProduct/ Applet: Skalarprodukt zweier Vektoren (engl./ free CDF-Player erforderlich) http://www.math.ethz.ch/~lemuren/public/exercise/linalg/LinearCombinationInR2ETHZ.html Applet: Linearkombination im zweidimensionalem Raum |
Hilfreiche Links
|
http://www.mathe-online.at/materialien/Andreas.Pester/files/Vectors/skalarprodukt_zweier_vektoren.htm Erläuterung zum Skalarprodukt |
Literatur
- Manfred Albach, Grundlagen der Elektrotechnik 1: Erfahrungssätze, Bauelemente, Gleichstromschaltungen, 3. Auflage (Pearson Studium, 2011)
- Kurt Meyberg and Peter Vachenauer, Höhere Mathematik 1: Differential- und Integralrechnung. Vektor- und Matrizenrechnung, 6. Auflage (Springer Berlin Heidelberg, 2001)
- Wolfgang Pavel and Ralf Winkler, Mathematik für Naturwissenschaftler, 1. Auflage (Pearson Studium, 2007)
- Anthony Croft and Robert Davison, Mathematics for Engineers: a modern interactive approach, 3. Auflage (Pearson-Prentice Hall, 2008)
| ← Zurück: Einfache Rechenoperationen mit Vektoren | Übersicht: Vektorrechnung | Vorwärts: Vektorprodukt → |
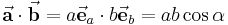
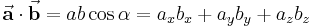
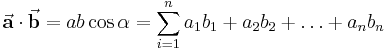
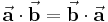
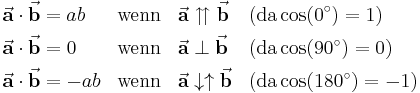
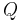 in einem homogenen elektrischen Feld
in einem homogenen elektrischen Feld 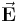 entlang einer geraden Strecke
entlang einer geraden Strecke 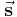 von einem Punkt
von einem Punkt 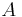 zu einem Punkt
zu einem Punkt 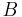 , so lässt sich die dabei aufgewendete Arbeit mit Hilfe des Skalarprodukts wie folgt bestimmen:
, so lässt sich die dabei aufgewendete Arbeit mit Hilfe des Skalarprodukts wie folgt bestimmen:
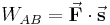
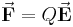 aufgebracht werden, das heißt in diesem Fall ergibt sich folgender Zusammenhang:
aufgebracht werden, das heißt in diesem Fall ergibt sich folgender Zusammenhang: