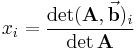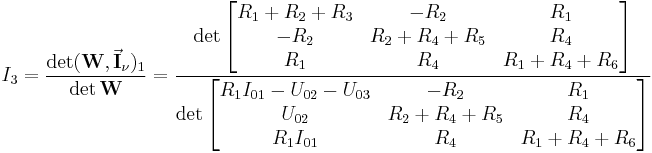Cramersche Regel: Unterschied zwischen den Versionen
| Zeile 28: | Zeile 28: | ||
\det | \det | ||
\begin{bmatrix} | \begin{bmatrix} | ||
| − | R_1 | + | R_1 I_{01} - U_{02} - U_{03} & -R_2 & R_1\\ |
| − | + | U_{02} & R_2 + R_4 + R_5 & R_4\\ | |
| − | R_1 & R_4 & R_1 + R_4 + R_6 | + | R_1 I_{01} & R_4 & R_1 + R_4 + R_6 |
\end{bmatrix} | \end{bmatrix} | ||
} | } | ||
Version vom 26. November 2012, 16:30 Uhr
|
|
Dieser Artikel befindet sich noch im Aufbau. |
| ← Zurück: Determinante einer quadratischen Matrix | Übersicht: Lineare Gleichungssysteme | Vorwärts: Übersicht Vektorrechnung → |
Die Cramersche Regel wird auch als Determinantenverfahren bezeichnet und stellt eine Methode zur Lösung linearer Gleichungssysteme dar. Die nachfolgenden Ausführungen beziehen sich zunächst auf ein allgemeines lineares Gleichungssystem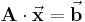 
, anschließend wird ein konkretes Beispiel betrachtet. Voraussetzung für die Anwendung des Verfahrens ist, dass die Koeffizientenmatrix 
quadratisch ist und ihre Determinante 
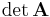nicht verschwindet (es muss also 
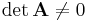gelten). Solche Gleichungssysteme ergeben sich beispielsweise im Rahmen einer Knoten- oder Maschenanalyse.
Die Cramersche Regel lautet dann wie folgt:
Dabei bezeichnet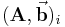 
die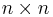 
-Matrix, bei der die 
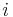-te Spalte von durch den Spaltenvektor 
ersetzt wurde. Das Element (die Komponente)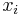 
des Vektors 
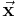ergibt sich dann aus dem Quotienten der Determinante von 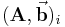und der Determinante von .
Zur Veranschaulichung der Regel wird nachfolgend das Beispiel aus der Einführung aufgegriffen:
Dieses Gleichungssystem der Form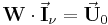 
wurde im Rahmen einer Maschenanalyse ermittelt und nachfolgend sollen die Ströme 
, 
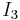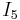und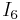 
bestimmt werden. Der Strom 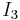ist das erste Element des Vektors mit den gesuchten Größen, somit ist auch zunächst die erste Spalte der Widerstandsmatrix 
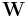durch den Quellspannungsvektor zu ersetzen, so dass folgt:
