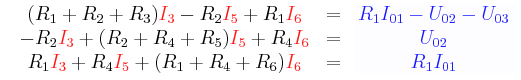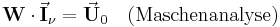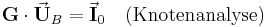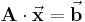Einführung zu linearen Gleichungssystemen

← Zurück: Übersicht zu linearen Gleichungssystemen

Übersicht: Lineare Gleichungssysteme

Vorwärts: Allgemeine Formulierung linearer Gleichungssysteme →

Ein Netzwerk aus linearen Zweipolen

Im Rahmen der Lehrveranstaltung werden lineare Gleichungssysteme (kurz LGS) zur Beschreibung linearer Netzwerke benötigt. Darunter versteht man eine beliebige Zusammenschaltung aktiver (z. B. Strom- und Spannungsquellen) und passiver (z. B. ohmsche Widerstände) linearer Zweipole. Ausgangspunkt zur Bestimmung solcher Gleichungssysteme sind in der Regel die Kirchhoffschen Gesetze, also Maschen- und Knotengleichungen. Möchte man nämlich 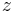$z$ unbekannte Größen (z. B. Spannungen) in einem Netzwerk bestimmen, so sind hierzu auch (mindestens) 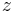$z$ linear unabhängige Gleichungen erforderlich. Die Verknüpfung dieser Gleichungen zu einem Gleichungssystem widerspiegelt die Tatsache, dass im Allgemeinen jeder Zweipol die Zweigspannungen und -ströme eines Netzwerks beeinflusst.

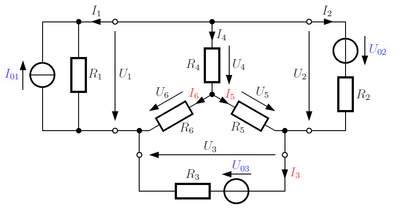
Durch eine systematische Vorgehensweise – nämlich der Knoten- und Maschenanalyse – lassen sich lineare Gleichungssysteme aufstellen, die eine gezielte Bestimmung von unbekannten Spannungen beziehungsweise Strömen in einem Netzwerk ermöglichen. Im Rahmen einer Maschenanalyse könnten zum Beispiel die folgenden drei Gleichungen ermittelt worden sein:

Dieses System aus linearen Gleichungen lässt sich auch in Matrixschreibweise angeben:

Bei der Schreibweise handelt es sich folglich um eine spezielle Darstellungsweise des Gleichungssystems, die weitere Berechnungen vereinfacht. Unter einer Matrix ist damit ein Zahlenschema zu verstehen, welches aus 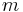$m$ Zeilen und 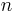$n$ Spalten besteht (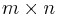$m\times n$-Matrix). Bezeichnet man die Widerstandsmatrix mit 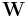$\textbf{W}$, den Vektor der Ströme in den Verbindungszweigen mit 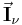$\vec{\textbf{I}}_\nu$ und den Quellspannungsvektor mit 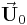$\vec{\textbf{U}}_0$, so folgt:

$\textbf{W} \cdot \vec{\textbf{I}}_\nu = \vec{\textbf{U}}_0 \quad (\text{Maschenanalyse})$

Die gesuchten Größen (im Rahmen der Maschenanalyse Ströme in den Verbindungszweigen) sind dabei die Komponenten des Vektors 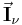$\vec{\textbf{I}}_\nu$. Mit Hilfe einer Knotenanalyse ist die gezielte Bestimmung der Spannungen in den Baumzweigen möglich, in diesem Fall erhält man in Matrixschreibweise:

$\textbf{G} \cdot \vec{\textbf{U}}_B = \vec{\textbf{I}}_0 \quad (\text{Knotenanalyse})$

Die Form des Gleichungssystems ändert sich also nicht, jedoch bezeichnet 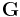$\textbf{G}$ nun die Leitwertmatrix (also eine Matrix mit Leitwerten), 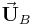$\vec{\textbf{U}}_B$ den Vektor der gesuchten Spannungen in den Baumzweigen und 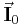$\vec{\textbf{I}}_0$ den Quellstromvektor. Aufgrund der Tatsache, dass zur Bestimmung von 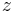$z$ unbekannten Größen auch (mindestens) 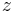$z$ linear unabhängige Gleichungen erforderlich sind, sind die in der Lehrveranstaltung vorkommenden Widerstands- und Leitwertmatrizen meist quadratisch. Das bedeutet, dass die Anzahl der Zeilen und Spalten gleich ist (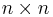$n\times n$-Matrix beziehungsweise $z\times z$-Matrix). In diesem Fall lassen sich die gesuchten Größen besonders einfach mit Hilfe der Cramerschen Regel bestimmen. Allgemein werden solche Gleichungssysteme in Matrixschreibweise meist wie folgt angegeben:

$\textbf{A} \cdot \vec{\textbf{x}} = \vec{\textbf{b}}$

In diesem Fall sind die gesuchten (unbekannten) Größen beziehungsweise Variablen die Komponenten des Vektors 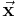$\vec{\textbf{x}}$. Dabei wird 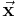$\vec{\textbf{x}}$ allgemein als Lösungs- oder Variablenvektor bezeichnet. Die Matrix $\textbf{A}$ wird allgemein als Koeffizientenmatrix und $\vec{\textbf{b}}$ zum Beispiel als Konstantenvektor oder schlicht „rechte Seite“ bezeichnet. Häufig werden in solchen Gleichungen auch die Vektorpfeile weggelassen, da ein Vektor auch als Spezialfall einer einspaltigen Matrix aufgefasst werden kann.