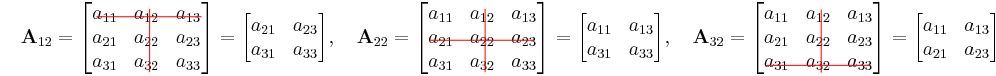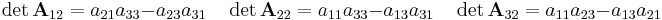Determinante
| ← Zurück: Lösung linearer Gleichungssysteme | Übersicht: Lineare Gleichungssysteme | Vorwärts: Cramersche Regel → |
Unter einer Determinante versteht man eine Zahl, die auf eindeutige Weise einer quadratischen Matrix zugeordnet werden kann. Die Zahl sagt etwas aus (determinieren = bestimmen/festlegen) über die Lösbarkeit eines linearen Gleichungssystems der Form 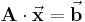 und spielt eine wichtige Rolle bei der Bestimmung der zugehörigen Lösung (vgl. Cramersche Regel). Die Ordnung einer Determinante entspricht der Anzahl der Zeilen (da sich der Begriff auf quadratische Matrizen bezieht stimmt diese mit der Anzahl der Spalten überein) der betrachteten Matrix. Ist die Determinante einer Matrix
und spielt eine wichtige Rolle bei der Bestimmung der zugehörigen Lösung (vgl. Cramersche Regel). Die Ordnung einer Determinante entspricht der Anzahl der Zeilen (da sich der Begriff auf quadratische Matrizen bezieht stimmt diese mit der Anzahl der Spalten überein) der betrachteten Matrix. Ist die Determinante einer Matrix  zu bestimmen, so wird dies durch folgende Schreibweisen gekennzeichnet:
zu bestimmen, so wird dies durch folgende Schreibweisen gekennzeichnet:
Neben der Verwendung des Operators 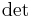 werden also auch häufig einfach Betragsstriche verwendet.
werden also auch häufig einfach Betragsstriche verwendet.
Es lässt sich zeigen, dass ein lineares Gleichungssystem genau dann eindeutig lösbar ist, wenn die Determinante der Koeffizientenmatrix  ungleich Null ist (es muss also
ungleich Null ist (es muss also 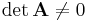 gelten). Ist dies nicht der Fall, so besitzt das Gleichungssystem unendlich viele Lösungen oder gar keine Lösung (die Zeilen von
gelten). Ist dies nicht der Fall, so besitzt das Gleichungssystem unendlich viele Lösungen oder gar keine Lösung (die Zeilen von  sind dann nicht linear unabhängig). Wurde das lineare Gleichungssystem im Rahmen einer Knoten- oder Maschenanalyse ermittelt, so ist dieses jedoch normalerweise eindeutig lösbar.
sind dann nicht linear unabhängig). Wurde das lineare Gleichungssystem im Rahmen einer Knoten- oder Maschenanalyse ermittelt, so ist dieses jedoch normalerweise eindeutig lösbar.
Determinanten zweiter Ordnung
Eine Determinante zweiter Ordnung bezieht sich auf eine 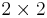 -Matrix. In diesem Fall kann die Determinante sofort angegeben werden, indem man die Produkte der Diagonalelemente wie folgt voneinander subtrahiert:
-Matrix. In diesem Fall kann die Determinante sofort angegeben werden, indem man die Produkte der Diagonalelemente wie folgt voneinander subtrahiert:
Ein einfaches Zahlenbeispiel für diesen Fall findet sich unten im Artikel Cramersche Regel.
Gegeben ist die nachfolgende Widerstandsmatrix, deren Determinante (beispielsweise zur Anwendung der Cramerschen Regel) bestimmt werden soll: Gemäß der obigen Vorschrift lässt sich das Ergebnis sofort angeben: |
Determinanten dritter Ordnung
Zur Bestimmung der Determinante einer  -Matrix ist die Regel von Sarrus (auch als Jägerzaun-Regel bekannt) ein hilfreiches Werkzeug. Zunächst schreibt man die ersten zwei Spalten erneut rechts neben die Matrix und verbindet die Diagonalen mit Linien, die die auszuführenden Rechenoperationen vorgeben:
-Matrix ist die Regel von Sarrus (auch als Jägerzaun-Regel bekannt) ein hilfreiches Werkzeug. Zunächst schreibt man die ersten zwei Spalten erneut rechts neben die Matrix und verbindet die Diagonalen mit Linien, die die auszuführenden Rechenoperationen vorgeben:
Die Determinante ergibt sich dann wie folgt aus den Diagonalelementen:
Gegeben ist eine Zunächst schreibt man die ersten zwei Spalten wieder rechts neben die Matrix und ergänzt gedanklich die oben eingezeichneten Linien. Damit folgt: Anschließend kann gemäß des obigen Schemas gerechnet werden und man erhält das Ergebnis: |
Determinanten höherer Ordnung
Zur Berechnung von Determinanten höherer Ordnung (Matrizen größer  ) kann zum Beispiel der Laplacesche Entwicklungssatz verwendet werden. Dieser stellt eine Rechenvorschrift dar, mit deren Hilfe durch Streichen von Zeilen und Spalten zunächst kleinere Teilmatrizen ermittelt werden, deren Determinanten wieder mit den obigen Regeln bestimmt werden können. Dabei lässt sich eine Determinante sowohl nach einer beliebig wählbaren Zeile als auch nach einer beliebig wählbaren Spalte „entwickeln“.
) kann zum Beispiel der Laplacesche Entwicklungssatz verwendet werden. Dieser stellt eine Rechenvorschrift dar, mit deren Hilfe durch Streichen von Zeilen und Spalten zunächst kleinere Teilmatrizen ermittelt werden, deren Determinanten wieder mit den obigen Regeln bestimmt werden können. Dabei lässt sich eine Determinante sowohl nach einer beliebig wählbaren Zeile als auch nach einer beliebig wählbaren Spalte „entwickeln“.
Für eine 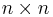 -Matrix gelten die folgenden Zusammenhänge:
-Matrix gelten die folgenden Zusammenhänge:
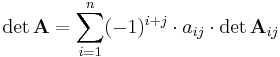 (Entwicklung nach der frei wählbaren Spalte
(Entwicklung nach der frei wählbaren Spalte 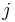 )
)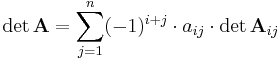 (Entwicklung nach der frei wählbaren Zeile
(Entwicklung nach der frei wählbaren Zeile 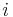 )
)
Dabei ist 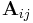 diejenige
diejenige 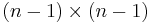 -Teilmatrix von
-Teilmatrix von 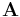 , die sich durch das Streichen der Zeile
, die sich durch das Streichen der Zeile 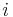 und der Spalte
und der Spalte 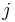 ergibt. Sind die sich ergebenden Teilmatrizen größer als
ergibt. Sind die sich ergebenden Teilmatrizen größer als  , so kann hierauf wiederum der Laplacesche Entwicklungssatz angewendet werden. Durch eine „geschickte“ Wahl der Entwicklungszeile beziehungweise -spalte können sich weitere Rechnungen vereinfachen.
, so kann hierauf wiederum der Laplacesche Entwicklungssatz angewendet werden. Durch eine „geschickte“ Wahl der Entwicklungszeile beziehungweise -spalte können sich weitere Rechnungen vereinfachen.
Der Laplacesche Entwicklungssatz gilt für beliebige quadratische Matrizen und damit auch für Jetzt wird nach der zweiten Spalte (also gilt Nun sind noch die Determinanten der Matrizen Die Determinanten dieser Teilmatrizen ergeben sich also wie folgt: Einsetzen liefert: Dieses Ergebnis bestätigt damit die Regel von Sarrus. |
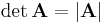

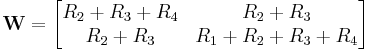
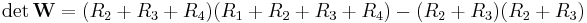

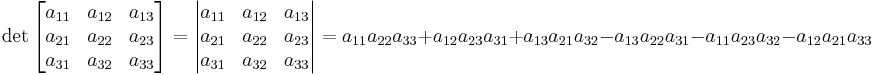
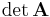 bestimmt werden soll:
bestimmt werden soll:
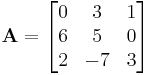

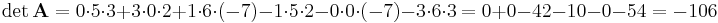

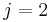 ) entwickelt (diese wurde willkürlich gewählt), so dass durch Einsetzen in die obige Beziehung folgt:
) entwickelt (diese wurde willkürlich gewählt), so dass durch Einsetzen in die obige Beziehung folgt:
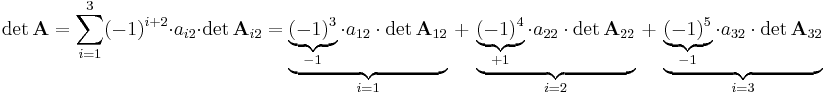
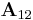 ,
, 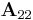 und
und 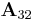 zu bestimmen. Dabei handelt es sich um die Teilmatrizen, die sich durch Streichen derjenigen Zeilen und Spalten ergeben, die durch die Indizes dieser Matrizen vorgegeben werden (
zu bestimmen. Dabei handelt es sich um die Teilmatrizen, die sich durch Streichen derjenigen Zeilen und Spalten ergeben, die durch die Indizes dieser Matrizen vorgegeben werden (