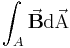Infinitesimale Weg-, Flächen-, und Volumenelemente

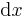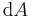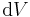Um über eine Fläche oder ein Volumen zu integrieren wird an das Integral ein Differential $\mathrm{d}x$,$\mathrm{d}A$ oder $\mathrm{d}V$ angehängt.

$\int_A\vec{\mathbf{B}}\mathrm{d}\vec{\mathrm{A}}$

$\int_V \rho\mathrm{d}V$

Die Bedeutung im eindimensionalen Fall ist noch recht simpel zu verstehen. Das Differential 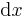$\mathrm{d}x$, welches schon aus der Schule bekannt sein sollte, hat eine eher Symbolische Bedeutung für einen infinitesimal kleines Wegelement. Betrachtet man nun aber das Differential einer Fläche oder eines Volumen, so ist deren Bedeutung etwas schwieriger zu fassen und auch die Transformation in verschiedene Koordinatensysteme ist nicht unbedingt trivial. Diese Eigenschaften sollen im folgenden bestimmt und verglichen werden.

Der einfachste Fall sind die kartesischen Koordinaten. Betrachtet man hier eine Integrationsfläche die sich in x-und y-Richtung ausbreitet. Ein infinitesimales Teilstück dieser Fläche muss dem zufolge auch in beide Richtungen ausgedehnt sein, um die gesamte Fläche beschreiben zu können. 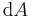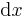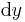Eine Integration über $\mathrm{d}A$, kann dann auch als Integration über beide Wegelemente $\mathrm{d}x$ und $\mathrm{d}y$ beschrieben werden, wie auch bei nicht infinitesimal kleinen Objekten die Fläche sich aus dem Produkt der Seiten bestimmt. Bei Volumen ist es im Grunde dasselbe, es muss nur auch noch die Ausdehnung in z berücksichtigt werden. Also ergibt sich ein infitesimales Volumenelement in kartesischen Koordinaten zu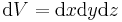 $\mathrm{d}V=\mathrm{d}x\mathrm{d}y\mathrm{d}z$

Schwieriger wird es, wenn die Wegelemente nicht mehr geradlinig verlaufen, dann müssen zur Berechnung der Flächen- und Volumenelemente so genannte Korrekturfaktoren eingeführt werden. Als Beispiel betrachtet man einen Kreisbogen in der x-y Ebene. Möchte man dort ein infinitesimales Flächenelement bestimmen so reicht es nicht aus einfach 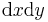$\mathrm{d}x\mathrm{d}y$ zu verwenden. Durch die Krümmung der Fläche würde der Fehler der dabei gemacht würde zu groß werden. Es bietet sich eine Koordinatentransformation in Polarkoordinaten an. Auf diese Weise kann entlang der Koordinatenlinien integriert werden, und man macht keinen Fehler. Zur Bestimmung des Korrekturfaktors betrachtet man nun ein Flächenelement des Kurvenstücks (vgl. Abbildung). Die Seitenlänge des Flächenelements entlang der r-Koordinate ist nicht gekrümmt und kann daher einfach als 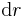$\mathrm{d}r$ angenommen werden. Betrachtet man jedoch die $\varphi$-Abhängigkeit so sieht man das die Krümmung des Kreisbogens nicht nur von $\varphi$ abhängt sondern auch von dem Radius r. Dies entspricht einer Umfangberechnung des Kreises. 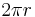Der Gesamtumfang eines Kreises hat $2\pi r$ betrachtet man allerdings nur ein kleines Teilstück des Kreises folgt: 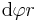$\mathrm{d}\varphi r$. Aus dieser Überlegung folgt das das infinitesimale Flächenelement einer Kreisfläche sich zu $\mathrm{d}A=r\mathrm{d}r\mathrm{d}\varphi$.

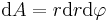Aus ähnlichen Betrachtungen ergeben sich die Volumenelemente, die in den Abbildungen zu sehen sind: