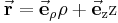Zylinderkoordinaten
Betrachtet man das Modell eines Kabels, ist es häufig problematisch Effekte mathematisch im gewohnten kartesischen Koordinatensystem zu beschreiben. Durch die Wölbung der Oberfläche muss im kartesischen System immer ein sich verändernder Winkel mitbetrachtet werden, selbst wenn die Effekte, die man beschreiben will senkrecht oder parallel zu dem Kabel verlaufen. Um sich die Rechnung zu vereinfachen, wählt man insbesondere für Probleme mit konzentrischen oder radialen Anordnungen einen Sonderfall der krummlinigen orthogonalen Koordinatensysteme, die Zylinderkoordinaten:
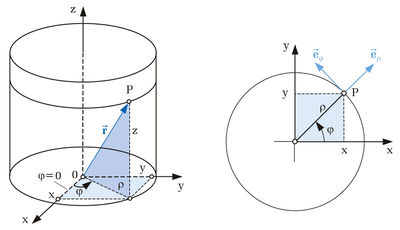
Um die Zylinderkoordinaten zu verstehen, hilft es sich einen Zylinder vorzustellen und ihn in seine Bestandteile, also Deckel und Mantelflächen zu unterteilen. Die Deckelfläche lässt sich dabei am einfachste mit ihren Radius 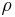 und dem Winkel
und dem Winkel  beschreiben ( siehe Abbildung). Eben diese Koordinaten werden bei den ebenen Zylinderkoordinaten oder Polarkoordinaten verwendet, dabei wird der Winkel
beschreiben ( siehe Abbildung). Eben diese Koordinaten werden bei den ebenen Zylinderkoordinaten oder Polarkoordinaten verwendet, dabei wird der Winkel  definitionsgemäß beginnend bei der positiven x-Achse entgegen dem Uhrzeigersinn gezählt.
Um auch noch die Höhe berücksichtigen zu können, wählt man die z-Koordinate, die schon aus den kartesischen Koordinaten bekannt ist. Diese entspricht auch der Länge der Mantelfläche des Zylinders. Mit diesen drei Koordinaten lässt sich jeder Raumpunkt erfassen.
definitionsgemäß beginnend bei der positiven x-Achse entgegen dem Uhrzeigersinn gezählt.
Um auch noch die Höhe berücksichtigen zu können, wählt man die z-Koordinate, die schon aus den kartesischen Koordinaten bekannt ist. Diese entspricht auch der Länge der Mantelfläche des Zylinders. Mit diesen drei Koordinaten lässt sich jeder Raumpunkt erfassen.
Aufgepasst:Im Gegensatz zu den Einheitsvektoren der kartesischen Koordinaten verändern die Einheitsvektoren der Zylinderkoordinaten ( und
und 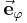 ) ihre Richtung mit Wachsenden Koordinatenwerten. Betrachtet man die Abbildung wird deutlich, dass
) ihre Richtung mit Wachsenden Koordinatenwerten. Betrachtet man die Abbildung wird deutlich, dass 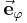 tangential zum Punkt P verläuft und
tangential zum Punkt P verläuft und  orthogonal.
orthogonal.
Zur Berechnung der Transformationsgleichungen verwendet man die Trigonometrischen Funktion. Als Beispiel soll die Koordinate x durch die Zylinder Koordinaten dargestellt werden. Dazu benötigt man nur die Parameter 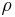 und
und  , da die z-Koordinate in beiden Systemen äquivalent ist. Betrachtet man nun die Abbildung, erkennt man, dass
, da die z-Koordinate in beiden Systemen äquivalent ist. Betrachtet man nun die Abbildung, erkennt man, dass 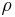 die Hypothenuse ist und x die Ankathete:
die Hypothenuse ist und x die Ankathete:
Stellt man nun nach x um erhält man die erste Transvormationsgleichung. Die zweite ergibt sich aus der selben Überlegung nur entspricht die y-Achse der Gegenkathete, daher erhält man den Sinus:
| Transformationsgleichung |
|
|
| |
|
|
Möchte man aus dem Zylinderkoordinatensystem wieder zurückrechnen in das kartesische Koordinatensystem muss man die oberen Tranformationsgleichungen umstellen und man erhält entsprechend:
| Transformationsgleichung |
|
|
| |
|
|
Nur die Transformationsgleichung reichen aber nicht, um die kartesischen Koordinaten durch Zylinderkoordinaten auszudrücken, da die Einheitsvektoren nach wie vor kartesisch dargestellt werden. Um auch sie umzuwandeln, kann man folgende Form verwenden:
Hier wird also der Ortsvektor (Ein Vektor, der vom Ursprung bis zu den Punkten im Raum verläuft. Die Berechnung des Ortsvektors wird im Beispiel veranschaulicht. Hier genügt es zu wissen, dass der Ortsvektor in kartesischen Koordinaten folgende Funktion besitzt: 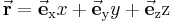 ) nach dem jeweiligen Koordinate abgeleitet und durch den Metrikooeffizienten geteilt.
Diese Formel wirkt auf dem ersten Blick schwer verständlich, betrachtet man ihre Funktion wird sie jedoch klarer: Die partielle Ableitung des Ortsvektors nach der jeweiligen Koordinate ist nichts weiter als die Änderungsgeschwindigkeit des Ortsvektors, also wie sehr sich dieser bei dem Verändern der Koordinate bewegt. Da Einheitsvektoren so definiert sind, dass sie immer die Länge 1 haben müssen. Wird der Einheitsvektor noch nomiert. Dies passiert durch den Metrikkoeffizienten, da dieser den Betrag der Änderung des Ortsvektors bestimmt. Übrig bleibt ein Vektor in Richtung der Änderung mit dem Betrag eins.
) nach dem jeweiligen Koordinate abgeleitet und durch den Metrikooeffizienten geteilt.
Diese Formel wirkt auf dem ersten Blick schwer verständlich, betrachtet man ihre Funktion wird sie jedoch klarer: Die partielle Ableitung des Ortsvektors nach der jeweiligen Koordinate ist nichts weiter als die Änderungsgeschwindigkeit des Ortsvektors, also wie sehr sich dieser bei dem Verändern der Koordinate bewegt. Da Einheitsvektoren so definiert sind, dass sie immer die Länge 1 haben müssen. Wird der Einheitsvektor noch nomiert. Dies passiert durch den Metrikkoeffizienten, da dieser den Betrag der Änderung des Ortsvektors bestimmt. Übrig bleibt ein Vektor in Richtung der Änderung mit dem Betrag eins.
Da die Gleichung trotzdem sehr unhandlich wirkt, ist die Rechnung hier durch ein Beispiel der Koordinate  aufgeschlüsselt. Zunächst wird der Metrikooeffizient berechnet, dazu müssen für die Variablen x,y,z die Transformationsgleichungen eingesetzt und nach der Koordinate
aufgeschlüsselt. Zunächst wird der Metrikooeffizient berechnet, dazu müssen für die Variablen x,y,z die Transformationsgleichungen eingesetzt und nach der Koordinate  differenziert werden. Anschließend wird der Betrag gebildet:
differenziert werden. Anschließend wird der Betrag gebildet:
Die beiden anderem Metrischen Koeffizienten ergeben sich zu:
Hat man nun die metrischen Faktoren kann man die Einheitsvektoren des Zylinderkoordinatensystems bestimmen, man muss nur noch, wie im Beispiel gezeigt den Ortsvektor nach der gesuchten Koordinate ableiten:
| Einheitsvektoren |
|
|
| |
|
|
Zwei weitere wichtige Parameter im Zylinderkoordinatensystem sind das vektorielle Wegelement :
und das Volumenelement:
Die Umwandlung von kartesischen Koordinaten in Zylinderkoordinaten ist nicht immer ganz einfach. Das sie sich trotzdem lohnt soll anhand dieses Beispiels verdeutlicht werden. Hier soll der Ortsvektor, eine einfache Funktion bei der der Vektor vom Koordinatenursprung auf einen Punkt abgebildet wird, in zylindrischen Koordinaten ausgedrückt werden. Da diese Darstellung viel übersichtlicher ist, als die in den kartesischen Koordinaten. Dafür sei der Ortsvektor Als erstes drückt man diesen Vektor in zylindrischen Koordinaten mithilfe der Transformationsgleichungen aus, und fasst die ersten beiden Terme zusammen: Vergleicht man die Beziehungen mit den Einheitsvektoren des Zylinderkoordinatensystems, sieht man sofort, dass die kartesischen Einheitsvektoren Durch einsetzen des Einheitsvektors |
Multimediale Lehrmaterialien
|
http://demonstrations.wolfram.com/ExploringCylindricalCoordinates/ Applet: Punkt in Zylinderkoordinaten (engl./ free CDF-Player erforderlich) http://demonstrations.wolfram.com/CylindricalCoordinates/ Applet: Punkt in Zylinderkoordinaten (engl./ free CDF-Player erforderlich) http://www.pha.jhu.edu/~javalab/cylindrical/cylindrical.html Applet: Punkt in Zylinderkoordinaten (engl.) |
Hilfreiche Links
|
http://scientificsentence.net/Electromagnetics/index.php?key=yes&Integer=Cylindrical Bild und Erläuterung zu den Einheitsvektoren im Zylinderkoordinatensystem (engl.) http://www.math.wpi.edu/Course_Materials/MA2251C99/images/cylndrcl.gif Bild zu infinitesimalen Volumenelement in Zylinderkoordinatensystem http://lh5.ggpht.com/_XvrTyMj5b-k/SaH0PTc-qWI/AAAAAAAAFnM/YYo0W-gT_5I/controlvolumecylindricalcontinuity5.png Bild zu einem infinitesimalen Volumenelement in Zylinderkoordinaten |
| ← Zurück: Das kartesische Koordinatensystem | Übersicht: Orthogonale Koordinatensysteme | Vorwärts: Kugelkoordinaten → |
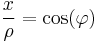
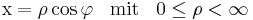
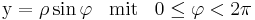
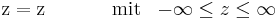
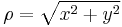
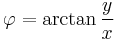

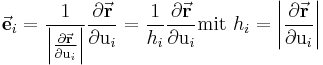
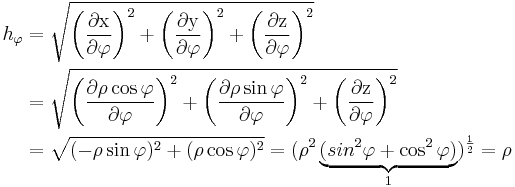
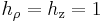
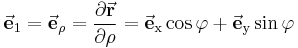
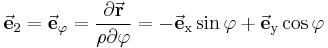

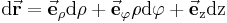
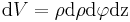
 in kartesischen Koordinaten gegeben:
in kartesischen Koordinaten gegeben:

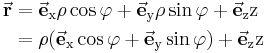
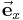 und
und 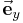 sich im zylindrischen System in dem Einheitsvektor
sich im zylindrischen System in dem Einheitsvektor 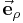 ausdrücken lassen:
ausdrücken lassen: