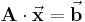|
|
| (6 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) |
| Zeile 1: |
Zeile 1: |
| − | {{Vorlage:Baustelle}} | + | {{Navigation|before=[[Einführung zu linearen Gleichungssystemen]]|overview=[[Lineare Gleichungssysteme:Übersicht|Lineare Gleichungssysteme]]|next=[[Einfache Rechenoperationen mit Matrizen]]}} |
| − | | |
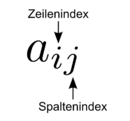
| | [[Datei:Indizes-matrix.png|130px|thumb|right|Bedeutung der Indizes bei Matrixelementen]] | | [[Datei:Indizes-matrix.png|130px|thumb|right|Bedeutung der Indizes bei Matrixelementen]] |
| | Im Rahmen der [[Einführung zu linearen Gleichungssystemen]] wurde bereits beschrieben, dass lineare Gleichungssysteme in Matrixschreibweise allgemein wie folgt angegeben werden können: | | Im Rahmen der [[Einführung zu linearen Gleichungssystemen]] wurde bereits beschrieben, dass lineare Gleichungssysteme in Matrixschreibweise allgemein wie folgt angegeben werden können: |
| Zeile 54: |
Zeile 53: |
| | | | |
| | Aufgrund der Tatsache, dass zur Bestimmung von <math>n</math> unbekannten Größen auch (mindestens) <math>n</math> [[linear unabhängige]] Gleichungen erforderlich sind, handelt es sich bei <math>\textbf{A}</math> häufig um eine ''quadratische'' Matrix. In diesem Fall gilt <math>m=n</math> und die Anzahl der Zeilen und Spalten ist folglich identisch (<math>n\times n</math>-Matrix). | | Aufgrund der Tatsache, dass zur Bestimmung von <math>n</math> unbekannten Größen auch (mindestens) <math>n</math> [[linear unabhängige]] Gleichungen erforderlich sind, handelt es sich bei <math>\textbf{A}</math> häufig um eine ''quadratische'' Matrix. In diesem Fall gilt <math>m=n</math> und die Anzahl der Zeilen und Spalten ist folglich identisch (<math>n\times n</math>-Matrix). |
| − |
| |
| − | ==Lösung linearer Gleichungssysteme==
| |
| − | Zur Lösung linearer Gleichungssysteme, also zur Bestimmung der Größen <math>x_1, x_2, \dots, x_n</math> beziehungsweise des Vektors <math>\vec{\textbf{x}}</math>, existiert eine Vielzahl von Verfahren. Handelt es sich bei <math>\textbf{A}</math> um eine quadratische Matrix, so kann beispielsweise die [[Cramersche Regel]] verwendet werden. Ausgangspunkt für die weiteren Betrachtungen ist zunächst eine Gleichung mit ausschließlich skalaren Größen <math>A</math>, <math>x</math> und <math>b</math>:
| |
| − | :<math>
| |
| − | Ax = b
| |
| − | </math>
| |
| − | Um in diesem Fall die Unbekannte <math>x</math> zu bestimmen, genügt eine Multiplikation der Gleichung mit <math>1/A=A^{-1}</math>:
| |
| − | :<math>
| |
| − | Ax = b\,|\cdot A^{-1}\quad\Rightarrow\quad \underbrace{A^{-1}\cdot A}_{1} x = A^{-1}\cdot b\quad\Rightarrow\quad x = A^{-1}\cdot b
| |
| − | </math>
| |
| − | Diese Vorgehensweise lässt sich auch auf lineare Gleichungssysteme in Matrixschreibweise übertragen. In diesem Fall benötigt man die sogenannte '''Inverse''' <math>\mathbf{A}^{-1}</math> zur Matrix <math>\mathbf{A}</math>. Das Produkt einer Matrix und der zugehörigen Inversen liefert dann die '''Einheitsmatrix''', die in der Regel mit <math>\mathbf{I}</math> oder <math>\mathbf{E}</math> bezeichnet wird. Bei der Einheitsmatrix handelt es sich um eine quadratische Matrix, bei der die Hauptdiagonale ausschließlich aus Einsen besteht, alle anderen Elemente sind 0 (vgl. Beispiel unten). Somit folgt:
| |
| − | :<math>
| |
| − | \mathbf{A}^{-1}\cdot\mathbf{A}= \mathbf{A}\cdot\mathbf{A}^{-1} = \mathbf{E}
| |
| − | </math>
| |
| − | Für das betrachtete lineare Gleichungssystem folgt also:
| |
| − | :<math>
| |
| − | \vec{\textbf{x}} = \mathbf{A}^{-1} \vec{\textbf{b}}
| |
| − | </math>
| |
| − | Es gilt zu beachten, dass nicht zu jeder Matrix eine Inverse existiert. Damit folgt auch, dass nicht jedes lineare Gleichungssystem eindeutig lösbar ist. Es lässt sich zeigen, dass ein lineares Gleichungssystem genau dann eindeutig lösbar ist, wenn die [[Determinante]] der Koeffizientenmatrix <math>\textbf{A}</math> ungleich Null ist (es muss also <math>\det\textbf{A} \neq 0</math> gelten, ansonsten ist das Gleichungssystem über- oder unterbestimmt). Genau dann ist die Matrix <math>\textbf{A}</math> auch invertierbar und genau dann sind auch die Gleichungen des linearen Gleichungssystems linear unabhängig. Es gilt zu beachten, dass die [[Multiplikation von Matrizen]] nicht kommutativ ist, das heißt die Reihenfolge der Faktoren hat einen Einfluss auf das Ergebnis. Daher wurde bei dem skalaren Beispiel schon darauf geachtet, dass die Gleichung ''auf beiden Seiten'' „von links“ mit <math>\mathbf{A}^{-1}</math> multipliziert wird.
| |
| − |
| |
| − | Die Bestimmung einer Inversen ist in der Regel sehr aufwändig und nur für den Fall einer <math>2\times 2</math>-Matrix noch mit überschaubarem Aufwand möglich. Dies gilt insbesondere dann, wenn die Komponenten (Einträge) der Matrix keine einfachen Zahlenwerte sondern Variablen (im Fall einer Widerstandsmatrix zum Beispiel Summen von Widerständen) sind. Daher werden solche Gleichungssysteme mit Hilfsmitteln wie der [[Cramersche Regel|Cramerschen Regel]] gelöst.
| |
| − |
| |
| − | {{Beispiel
| |
| − | |Titel=Einfaches Zahlenbeispiel
| |
| − | |Inhalt=
| |
| − | Gegeben ist das nachfolgende lineare Gleichungssystem, welches mit der oben beschriebenen Methode gelöst werden soll:
| |
| − | :<math>
| |
| − | \begin{bmatrix}4 & 2\\10 & 6\end{bmatrix}
| |
| − | \begin{bmatrix}x_1\\x_2\end{bmatrix}=
| |
| − | \begin{bmatrix}8\\12\end{bmatrix}
| |
| − | </math>
| |
| − | Zunächst ist die Inverse <math>\mathbf{A}^{-1}</math> der Koeffizientenmatrix <math>\mathbf{A}</math> zu bestimmen. Für <math>2\times 2</math>-Matrizen (bei größeren Matrizen ist der Aufwand wesentlich höher) gilt:
| |
| − | :<math>
| |
| − | \mathbf{A}^{-1} =
| |
| − | \begin{bmatrix}
| |
| − | a_{11} & a_{12}\\ a_{21} & a_{22} \\
| |
| − | \end{bmatrix}^{-1} =
| |
| − | \frac{1}{\det\mathbf{A}} \begin{bmatrix}
| |
| − | a_{22} & -a_{12}\\ -a_{21} & a_{11} \\
| |
| − | \end{bmatrix} =
| |
| − | \frac{1}{a_{11}a_{22}-a_{12}a_{21}} \begin{bmatrix}
| |
| − | a_{22} & -a_{12}\\ -a_{21} & a_{11} \\
| |
| − | \end{bmatrix}
| |
| − | </math>
| |
| − | Für das Beispiel folgt damit:
| |
| − | :<math>
| |
| − | \begin{bmatrix}4 & 2\\10 & 6\end{bmatrix}^{-1} =
| |
| − | \frac{1}{4\cdot 6-2\cdot 10}
| |
| − | \begin{bmatrix}6 & -2\\-10 & 4\end{bmatrix}
| |
| − | =
| |
| − | \frac{1}{4}
| |
| − | \begin{bmatrix}6 & -2\\-10 & 8\end{bmatrix}
| |
| − | =
| |
| − | \begin{bmatrix}\frac{6}{4} & \frac{-2}{4}\\\frac{-10}{4} & \frac{8}{4}\end{bmatrix}
| |
| − | =
| |
| − | \begin{bmatrix}\frac{3}{2} & \frac{-1}{2}\\\frac{-5}{2} & \frac{4}{2}\end{bmatrix}
| |
| − | </math>
| |
| − | Nun kann das lineare Gleichungssystem in Matrixschreibweise von links mit der Inversen [[Multiplikation von Matrizen|multipliziert]] werden:
| |
| − | :<math>
| |
| − | \begin{bmatrix}\frac{3}{2} & \frac{-1}{2}\\\frac{-5}{2} & \frac{4}{2}\end{bmatrix}\cdot
| |
| − | \begin{bmatrix}4 & 2\\10 & 6\end{bmatrix}
| |
| − | \begin{bmatrix}x_1\\ x_2\end{bmatrix}
| |
| − | =
| |
| − | \begin{bmatrix}\frac{3}{2} & \frac{-1}{2}\\\frac{-5}{2} & \frac{4}{2}\end{bmatrix}\cdot
| |
| − | \begin{bmatrix}8\\12\end{bmatrix}
| |
| − | </math>
| |
| − | Nach der [[Multiplikation von Matrizen|Multiplikation der Matrizen]] folgt:
| |
| − | :<math>
| |
| − | \begin{bmatrix}1&0\\0&1\end{bmatrix}
| |
| − | \begin{bmatrix}x_1\\ x_2\end{bmatrix}
| |
| − | =
| |
| − | \begin{bmatrix}x_1\\ x_2\end{bmatrix}
| |
| − | =
| |
| − | \begin{bmatrix}6\\ -8\end{bmatrix}
| |
| − | </math>
| |
| − | Damit folgt also <math>x_1=6</math> und <math>x_2=-8</math>. Die Richtigkeit dieses Ergebnisses kann leicht durch Einsetzen überprüft werden (Probe).
| |
| − |
| |
| − | Mit Hilfe der [[Cramersche Regel|Cramerschen Regel]] lässt sich die Lösung einfacher bestimmen, dies wird in dem [[Cramersche Regel|zugehörigen Artikel]] beschrieben.
| |
| − | }}
| |
| | | | |
| | [[Kategorie:Artikel]] | | [[Kategorie:Artikel]] |
| | [[Kategorie:Feedback]] | | [[Kategorie:Feedback]] |
Dabei handelt es sich um eine spezielle Schreibweise eines Systems (also mehrerer zusammengehöriger) linearer Gleichungen. Im allgemeinsten Fall liegt ein System aus 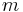 linearen Gleichungen mit
linearen Gleichungen mit 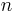 unbekannten Variablen
unbekannten Variablen 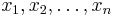 vor:
vor:
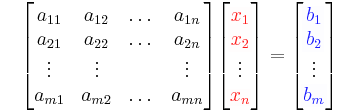
In Matrixschreibweise kann das lineare Gleichungssystem wie folgt angegeben werden:
 : Koeffizientenmatrix
: Koeffizientenmatrix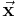 : Lösungs- oder Variablenvektor (enthält die gesuchten Variablen)
: Lösungs- oder Variablenvektor (enthält die gesuchten Variablen) : Konstantenvektor oder „rechte Seite“
: Konstantenvektor oder „rechte Seite“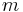 linearen Gleichungen mit
linearen Gleichungen mit 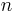 unbekannten Variablen
unbekannten Variablen 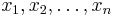 vor:
vor:
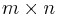 -Matrix
-Matrix  werden also mit
werden also mit 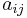 bezeichnet, wobei
bezeichnet, wobei 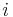 die Zeile und
die Zeile und 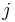 die Spalte des betrachteten Elements angibt (vgl. Abbildung).
die Spalte des betrachteten Elements angibt (vgl. Abbildung).
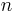 unbekannten Größen auch (mindestens)
unbekannten Größen auch (mindestens) 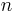 linear unabhängige Gleichungen erforderlich sind, handelt es sich bei
linear unabhängige Gleichungen erforderlich sind, handelt es sich bei  häufig um eine quadratische Matrix. In diesem Fall gilt
häufig um eine quadratische Matrix. In diesem Fall gilt 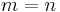 und die Anzahl der Zeilen und Spalten ist folglich identisch (
und die Anzahl der Zeilen und Spalten ist folglich identisch (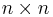 -Matrix).
-Matrix).