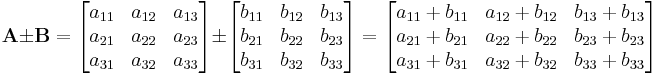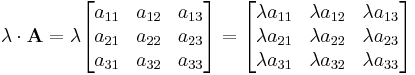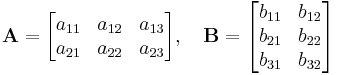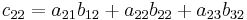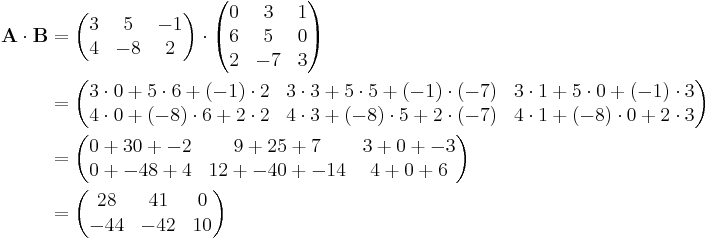Einfache Rechenoperationen mit Matrizen
| ← Zurück: Allgemeine Formulierung linearer Gleichungssysteme | Übersicht: Lineare Gleichungssysteme | Vorwärts: Lösung linearer Gleichungssysteme → |
Bei der Rechnung mit Matrizen gelten häufig die Gesetzmäßigkeiten aus der Vektorrechnung. Dies ist plausibel, da ein Vektor auch als Spezialfall einer Matrix mit nur einer Spalte aufgefasst werden kann. Lediglich bei der Multiplikation von Matrizen unterscheidet sich das Vorgehen.
Inhaltsverzeichnis
Addition und Subtraktion von Matrizen
Sollen zwei Matrizen addiert oder subtrahiert werden, so müssen diese die gleiche Anzahl an Zeilen und Spalten haben. Formal formuliert können also nur dann zwei 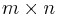 Matrizen addiert oder subtrahiert werden, wenn
Matrizen addiert oder subtrahiert werden, wenn 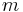 und
und 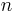 jeweils gleich sind. Die Berechnung der Summe beziehungsweise Differenz erfolgt durch die Addition beziehungsweise Subtraktion der jeweils zusammengehörigen Einträge.
jeweils gleich sind. Die Berechnung der Summe beziehungsweise Differenz erfolgt durch die Addition beziehungsweise Subtraktion der jeweils zusammengehörigen Einträge.
Beispiel für zwei  -Matrizen
-Matrizen 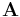 und
und 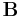 :
:
Die Reihenfolge, in der die Rechnung ausgeführt wird, spielt damit keine Rolle. Damit gilt das Kommutativgesetz, das heißt 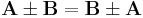 .
.
Multiplikation von Matrizen mit einem Skalar
Bei der Multiplikation einer Matrix mit einem Skalar wird jedes Element der Matrix mit dem Skalar multipliziert.
Beispiel für eine  -Matrix
-Matrix 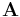 und einem Skalar
und einem Skalar 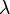 :
:
Division von Matrizen
Ähnlich wie bei der Vektorrechnung ist die Division von Matrizen nicht definiert. Jedoch existiert der Begriff der Inversen einer Matrix, mit dessen Hilfe eine Division auf eine Multiplikation zurückgeführt werden kann.
Multiplikation von Matrizen
Zwei Matrizen lassen sich nur dann miteinander multiplizieren, wenn die Anzahl der Spalten der ersten Matrix mit der Anzahl der Zeilen der zweiten Matrix übereinstimmt. Handelt es sich um eine 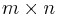 -Matrix
-Matrix 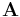 und eine
und eine 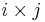 -Matrix
-Matrix 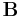 , so liefert das Produkt
, so liefert das Produkt  dieser beiden Matrizen eine
dieser beiden Matrizen eine 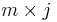 -Matrix (also eine Matrix mit
-Matrix (also eine Matrix mit 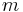 Zeilen und
Zeilen und 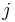 Spalten).
Spalten).
Eine übersichtliche Möglichkeit zur Matrizenmultiplikation ist die Anwendung des Falkschen Schemas. Zur Berechnung des Produkts  notiert man zunächst die Matrix
notiert man zunächst die Matrix 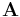 und rechts darüber die Matrix
und rechts darüber die Matrix 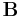 . Zur Bestimmung eines Eintrags der resultierenden Matrix bildet man dann das Skalarprodukt aus dem kreuzenden Zeilenvektor von
. Zur Bestimmung eines Eintrags der resultierenden Matrix bildet man dann das Skalarprodukt aus dem kreuzenden Zeilenvektor von 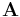 und dem Spaltenvektor von
und dem Spaltenvektor von 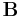 .
.
Betrachtet werden nun die folgenden beiden Matrizen:
Damit ergibt sich das folgende Falksche Schema:
Das Element 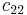 der resultierenden Matrix ergibt sich damit wie folgt (Skalarprodukt):
der resultierenden Matrix ergibt sich damit wie folgt (Skalarprodukt):
Die weiteren Elemente der resultierenden Matrix lassen sich auf die gleiche Weise bestimmen. Es gilt zu beachten, dass die Matrizenmultiplikation nicht kommutativ ist, also 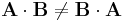 .
.
Rechengesetze
Für drei Matrizen 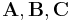 folgt:
folgt:
Das Kommutativgesetz gilt nicht: 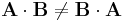
Distributivgesetz: 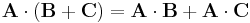
Assoziativgesetz: