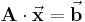Allgemeine Formulierung linearer Gleichungssysteme: Unterschied zwischen den Versionen
K (Schützte „Allgemeine Formulierung linearer Gleichungssysteme“ ([Bearbeiten=Nur Administratoren erlauben] (unbeschränkt) [Verschieben=Nur Administratoren erlauben] (unbeschränkt))) |
|||
| (105 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | {{ | + | {{Navigation|before=[[Einführung zu linearen Gleichungssystemen]]|overview=[[Lineare Gleichungssysteme:Übersicht|Lineare Gleichungssysteme]]|next=[[Einfache Rechenoperationen mit Matrizen]]}} |
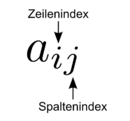
| − | + | [[Datei:Indizes-matrix.png|130px|thumb|right|Bedeutung der Indizes bei Matrixelementen]] | |
| − | Im Rahmen der [[Einführung zu linearen Gleichungssystemen]] wurde bereits beschrieben, dass | + | Im Rahmen der [[Einführung zu linearen Gleichungssystemen]] wurde bereits beschrieben, dass lineare Gleichungssysteme in Matrixschreibweise allgemein wie folgt angegeben werden können: |
:<math> | :<math> | ||
\textbf{A} \cdot \vec{\textbf{x}} = \vec{\textbf{b}} | \textbf{A} \cdot \vec{\textbf{x}} = \vec{\textbf{b}} | ||
</math> | </math> | ||
| − | Dabei werden | + | Dabei werden die nachstehenden Bezeichnungen verwendet: |
:<math>\textbf{A}</math>: Koeffizientenmatrix | :<math>\textbf{A}</math>: Koeffizientenmatrix | ||
:<math>\vec{\textbf{x}}</math>: Lösungs- oder Variablenvektor (enthält die gesuchten Variablen) | :<math>\vec{\textbf{x}}</math>: Lösungs- oder Variablenvektor (enthält die gesuchten Variablen) | ||
:<math>\vec{\textbf{b}}</math>: Konstantenvektor oder „rechte Seite“ | :<math>\vec{\textbf{b}}</math>: Konstantenvektor oder „rechte Seite“ | ||
| − | Dabei handelt es sich | + | Dabei handelt es sich um eine spezielle Schreibweise eines Systems (also mehrerer zusammengehöriger) linearer Gleichungen. Im allgemeinsten Fall liegt ein System aus <math>m</math> linearen Gleichungen mit <math>n</math> unbekannten Variablen <math>x_1, x_2, \dots, x_n</math> vor: |
| + | |||
| + | <!-- | ||
:<math> | :<math> | ||
\begin{matrix} | \begin{matrix} | ||
a_{11}x_1 + a_{12}x_2 \, + & \cdots & +\, a_{1n}x_n & = & b_1\\ | a_{11}x_1 + a_{12}x_2 \, + & \cdots & +\, a_{1n}x_n & = & b_1\\ | ||
a_{21}x_1 + a_{22}x_2 \, + & \cdots & +\, a_{2n}x_n & = & b_2\\ | a_{21}x_1 + a_{22}x_2 \, + & \cdots & +\, a_{2n}x_n & = & b_2\\ | ||
| − | \vdots &&&\vdots | + | \vdots\quad\quad\quad\vdots\quad&&\quad\vdots&&\vdots\\ |
a_{m1}x_1 + a_{m2}x_2 \, + & \cdots & +\, a_{mn}x_n & = & b_m\\ | a_{m1}x_1 + a_{m2}x_2 \, + & \cdots & +\, a_{mn}x_n & = & b_m\\ | ||
\end{matrix} | \end{matrix} | ||
</math> | </math> | ||
| + | --> | ||
| + | [[Datei:Lgs-allgemein-gleichungen.png|Gleichungen eines allgemeinen linearen Gleichungssystems]] | ||
| + | |||
In Matrixschreibweise kann das lineare Gleichungssystem wie folgt angegeben werden: | In Matrixschreibweise kann das lineare Gleichungssystem wie folgt angegeben werden: | ||
| + | |||
| + | <!-- | ||
:<math> | :<math> | ||
\begin{bmatrix} | \begin{bmatrix} | ||
| Zeile 29: | Zeile 36: | ||
x_1\\ | x_1\\ | ||
x_2\\ | x_2\\ | ||
| − | \ | + | \vdots\\ |
x_n | x_n | ||
| + | \end{bmatrix} | ||
| + | = | ||
| + | \begin{bmatrix} | ||
| + | b_1\\ | ||
| + | b_2\\ | ||
| + | \vdots\\ | ||
| + | b_m | ||
\end{bmatrix} | \end{bmatrix} | ||
</math> | </math> | ||
| + | --> | ||
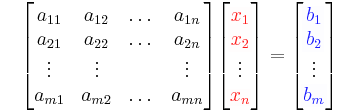
| + | [[Datei:Lgs-allgemein-matrixschreibweise.png|Allgemeines lineares Gleichungssystem in Matrixschreibweise]] | ||
| + | |||
| + | Die Elemente (Einträge) der <math>m\times n</math>-Matrix <math>\textbf{A}</math> werden also mit <math>a_{ij}</math> bezeichnet, wobei <math>i</math> die Zeile und <math>j</math> die Spalte des betrachteten Elements angibt (vgl. Abbildung). | ||
| + | |||
| + | Aufgrund der Tatsache, dass zur Bestimmung von <math>n</math> unbekannten Größen auch (mindestens) <math>n</math> [[linear unabhängige]] Gleichungen erforderlich sind, handelt es sich bei <math>\textbf{A}</math> häufig um eine ''quadratische'' Matrix. In diesem Fall gilt <math>m=n</math> und die Anzahl der Zeilen und Spalten ist folglich identisch (<math>n\times n</math>-Matrix). | ||
[[Kategorie:Artikel]] | [[Kategorie:Artikel]] | ||
[[Kategorie:Feedback]] | [[Kategorie:Feedback]] | ||
Aktuelle Version vom 14. Januar 2015, 20:57 Uhr
| ← Zurück: Einführung zu linearen Gleichungssystemen | Übersicht: Lineare Gleichungssysteme | Vorwärts: Einfache Rechenoperationen mit Matrizen → |
Im Rahmen der Einführung zu linearen Gleichungssystemen wurde bereits beschrieben, dass lineare Gleichungssysteme in Matrixschreibweise allgemein wie folgt angegeben werden können:
Dabei werden die nachstehenden Bezeichnungen verwendet:
 : Koeffizientenmatrix
: Koeffizientenmatrix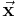 : Lösungs- oder Variablenvektor (enthält die gesuchten Variablen)
: Lösungs- oder Variablenvektor (enthält die gesuchten Variablen) : Konstantenvektor oder „rechte Seite“
: Konstantenvektor oder „rechte Seite“
Dabei handelt es sich um eine spezielle Schreibweise eines Systems (also mehrerer zusammengehöriger) linearer Gleichungen. Im allgemeinsten Fall liegt ein System aus 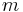 linearen Gleichungen mit
linearen Gleichungen mit 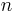 unbekannten Variablen
unbekannten Variablen 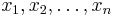 vor:
vor:
In Matrixschreibweise kann das lineare Gleichungssystem wie folgt angegeben werden:
Die Elemente (Einträge) der 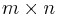 -Matrix
-Matrix  werden also mit
werden also mit 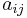 bezeichnet, wobei
bezeichnet, wobei 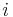 die Zeile und
die Zeile und 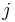 die Spalte des betrachteten Elements angibt (vgl. Abbildung).
die Spalte des betrachteten Elements angibt (vgl. Abbildung).
Aufgrund der Tatsache, dass zur Bestimmung von 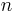 unbekannten Größen auch (mindestens)
unbekannten Größen auch (mindestens) 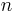 linear unabhängige Gleichungen erforderlich sind, handelt es sich bei
linear unabhängige Gleichungen erforderlich sind, handelt es sich bei  häufig um eine quadratische Matrix. In diesem Fall gilt
häufig um eine quadratische Matrix. In diesem Fall gilt 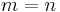 und die Anzahl der Zeilen und Spalten ist folglich identisch (
und die Anzahl der Zeilen und Spalten ist folglich identisch (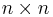 -Matrix).
-Matrix).