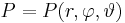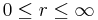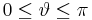Orthogonale Koordinatensysteme:Übersicht: Unterschied zwischen den Versionen
| Zeile 49: | Zeile 49: | ||
<math>P=P(\rho,\varphi,z)</math><br> | <math>P=P(\rho,\varphi,z)</math><br> | ||
<math>0 \leq \rho \leq\infty</math><br> | <math>0 \leq \rho \leq\infty</math><br> | ||
| − | <math>0 \leq \varphi | + | <math>0 \leq \varphi < 2\pi</math><br> |
<math>-\infty \leq z \leq\infty</math> | <math>-\infty \leq z \leq\infty</math> | ||
|style="background-color:#dde6f3"|[[Image:Koordinatensysteme_Krummlinige_Koordinaten3.jpg|center|miniatur|Zylinderkoordinaten]] | |style="background-color:#dde6f3"|[[Image:Koordinatensysteme_Krummlinige_Koordinaten3.jpg|center|miniatur|Zylinderkoordinaten]] | ||
| Zeile 58: | Zeile 58: | ||
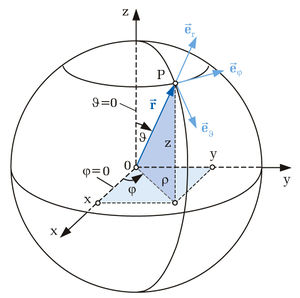
<math>P=P(r,\varphi,\vartheta)</math> | <math>P=P(r,\varphi,\vartheta)</math> | ||
<math>0\leq r\leq\infty</math><br> | <math>0\leq r\leq\infty</math><br> | ||
| − | <math>0\leq \varphi | + | <math>0\leq \varphi < 2\pi</math><br> |
<math>0\leq \vartheta\leq\pi</math> | <math>0\leq \vartheta\leq\pi</math> | ||
|style="background-color:#dde6f3"|[[Image:Koordinatensysteme_Krummlinige_Koordinaten4.jpg|center|miniatur|Kugelkoordinaten]] | |style="background-color:#dde6f3"|[[Image:Koordinatensysteme_Krummlinige_Koordinaten4.jpg|center|miniatur|Kugelkoordinaten]] | ||
|} | |} | ||
Version vom 3. August 2012, 15:48 Uhr
To-do:
- Einleitung hinzufügen
- Formulierungen überarbeiten (insbes. fett und diejenigen in der Tabelle)
- Hinweis, dass rho in ZK auch oft mit r bezeichnet wird
- Angeben, dass kartesisches System immer als Referenz dient
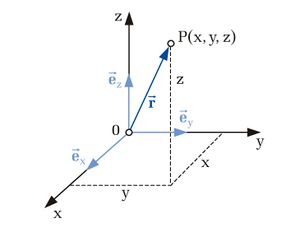
| Kartesische Koordinaten
Bei dem kartesischen Koordinatensystem wird ein Punkt |
|
|
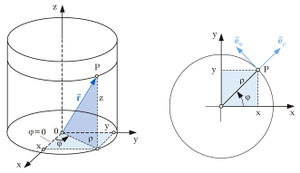
| Zylinderkoordinaten
Bei den Zylinderkoordinaten wird ein Punkt |
|
|
| Kugelkoordinaten
Bei dem Kugelkoordinatensystem wird ein Punkt |
|
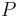 im Raum durch die drei Koordinaten
im Raum durch die drei Koordinaten  ,
, 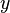 und
und 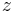 beschrieben. Die Koordinatenachsen sind geradlinig und orthogonal zueinander angeordnet, so dass diese ein
beschrieben. Die Koordinatenachsen sind geradlinig und orthogonal zueinander angeordnet, so dass diese ein 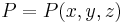
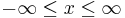

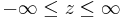
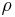 ,
,  und
und 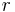 bezeichnet) gibt den Abstand zur
bezeichnet) gibt den Abstand zur 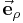 und
und 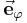 hängt von der Position des betrachteten Punktes ab. Betrachtet man ausschließlich die
hängt von der Position des betrachteten Punktes ab. Betrachtet man ausschließlich die 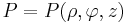
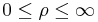
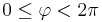
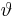 beschrieben. Dabei bezeichnet
beschrieben. Dabei bezeichnet 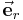 ,
, 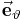 hängt stets von der Position des betrachteten Punktes ab. Alle Punkte mit identischem Winkel
hängt stets von der Position des betrachteten Punktes ab. Alle Punkte mit identischem Winkel