Zylinderkoordinaten: Unterschied zwischen den Versionen
| Zeile 69: | Zeile 69: | ||
\left( \frac{\partial \mathrm{z}}{\partial \mathrm{\varphi}} \right)^2}\\ | \left( \frac{\partial \mathrm{z}}{\partial \mathrm{\varphi}} \right)^2}\\ | ||
& =\sqrt{(-\rho\sin\varphi)^2+(\rho\cos\varphi)^2} | & =\sqrt{(-\rho\sin\varphi)^2+(\rho\cos\varphi)^2} | ||
| − | =\sqrt{\rho^2(sin^2\varphi+\cos^2\varphi)}=\rho | + | =\sqrt{\rho^2\underbrace {(sin^2\varphi+\cos^2\varphi)}_{1}}=\rho |
\end{align} | \end{align} | ||
</math> | </math> | ||
Version vom 12. April 2012, 15:35 Uhr
Betrachtet man das Modell eines Kabels, ist es häufig problematisch Effekte mathematisch im gewohnten kartesischen Koordinatensystem zu beschreiben. Durch die Wölbung der Oberfläche bekommt man im kartesischen System immer eine Winkelabhängigkeit, selbst wenn die Effekte, die man beschreiben will senkrecht oder parallel zu dem Kabel verlaufen. Um sich die Rechnung zu vereinfachen wählt man insbesondere für Probleme mit konzentrischen oder radialen Anordnungen einen Sonderfall der krummlinigen orthogonalen Koordinatensysteme, die Zylinderkoordinaten:
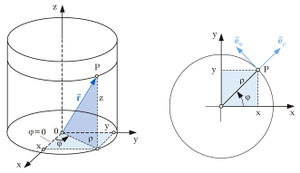
Um die Zylinderkoordinaten zu verstehen, hilft es sich einen Zylinder vorzustellen und ihn in seine Bestandteile, also Deckel und Mantelflächen zu unterteilen. Die Deckelfläche lässt sich dabei am einfachste mit ihren Radius 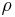 und dem Winkel
und dem Winkel  beschreiben ( siehe Abbildung). Eben diese Koordinaten werden bei den ebenen Zylinderkoordinaten oder Polarkoordinaten verwendet, dabei wird der Winkel
beschreiben ( siehe Abbildung). Eben diese Koordinaten werden bei den ebenen Zylinderkoordinaten oder Polarkoordinaten verwendet, dabei wird der Winkel  definitionsgemäß beginnend bei der positiven x-Achse entgegen dem Uhrzeigersinn gezählt. Um auch noch die Höhe berücksichtigen zu können, wählt man die z-Koordinate, die schon aus den kartesischen Koordinaten bekannt ist. Diese entspricht auch der Länge der Mantelfläche des Zylinders. Mit diesen drei Koordinaten lässt sich jeder Raumpunkt erfassen.
definitionsgemäß beginnend bei der positiven x-Achse entgegen dem Uhrzeigersinn gezählt. Um auch noch die Höhe berücksichtigen zu können, wählt man die z-Koordinate, die schon aus den kartesischen Koordinaten bekannt ist. Diese entspricht auch der Länge der Mantelfläche des Zylinders. Mit diesen drei Koordinaten lässt sich jeder Raumpunkt erfassen.
Betrachtet man die Abbildung, kann man mithilfe der Trigonometrischen Funktionen die Transformationsgleichung berechnen:
Möchte man die Koordinate x durch die Zylinder Koordinaten darstellen. Muss man sich nur die Parameter 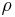 und
und  betrachten, da die z-Koordinate in beiden Systemen äquivalent ist. Betrachtet man nun die Abbildung, sieht man, dass wenn
betrachten, da die z-Koordinate in beiden Systemen äquivalent ist. Betrachtet man nun die Abbildung, sieht man, dass wenn 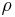 die Hypothenuse ist und x die Ankathete, kann man mit Hilfe der trigonometrischen Form:
die Hypothenuse ist und x die Ankathete, kann man mit Hilfe der trigonometrischen Form: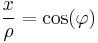 Stellt man nun nach x um erhält man die erste Transvormationsgleichung. Die zweite ergibt sich aus der selben Überlegung nur entspricht die y-Achse der Gegenkathete, daher erhält man den Sinus:
Stellt man nun nach x um erhält man die erste Transvormationsgleichung. Die zweite ergibt sich aus der selben Überlegung nur entspricht die y-Achse der Gegenkathete, daher erhält man den Sinus:
| Transformationsgleichung |
|
|
| |
|
|
Berechnet man die Transformationsgleichung vom Zylinderkoordinatensystem ins kartesische Koordinatensystem folgt:
Die Metrikkoeffizienten oder metrischen Faktoren berechnen sich durch folgende Gleichung:
Sie werden benötigt, damit die Einheitsvektoren in das jeweilige System transformiert werden können. Da die Gleichung sehr unhandlich wirkt ist die Rechnung hier durch ein Beispiel der Koordinate  aufgeschlüsselt. Dazu müssen für die Variablen x,y,z die Transformationsgleichungen eingesetzt und nach der Koordinate differenziert werden. Anschließend wird der Betrag gebildet:
aufgeschlüsselt. Dazu müssen für die Variablen x,y,z die Transformationsgleichungen eingesetzt und nach der Koordinate differenziert werden. Anschließend wird der Betrag gebildet:
Die beiden anderem Metrischen Koeffizienten ergeben sich zu:
Hat man nun die metrischen Faktoren kann man die Einheitsvektoren des Zylinderkoordinatensystems bestimmen:
Zwei weitere wichtige Parameter im Zylinderkoordinatensystem sind das vektorielle Wegelement :
und das Volumenelement:
Eine anschauliche Funktion wird durch den Ortsvektor beschrieben. Dabei wird vom Koordinatenursprung ein Vektor auf einen Punkt abgebildet. Hier soll geziegt werden, dass es in diesem Fall einfacher ist, den Ortsvektor in zylindrischen Koordinaten auszudrücken, als in den kartesischen Koordinaten. Dafür sei der Ortsvektor Als erstes drückt man diesen Vektor in zylindrischen Koordinaten mithilfe der Transformationsgleichungen aus, und fasst die ersten beiden Terme zusammen: Vergleicht man die Beziehungen mit den Einheitsvektoren des Zylinderkoordinatensystems, sieht man sofort, dass die kartesischen Einheitsvektoren Durch diesen Koeffizientenvergleich erhält man die folgende, viel einfachere Darstellung des Ortsvektors in Zylinderkoordinaten: |
Multimediale Lehrmaterialien
|
http://demonstrations.wolfram.com/ExploringCylindricalCoordinates/ Applet: Punkt in Zylinderkoordinaten (engl./ free CDF-Player erforderlich) http://demonstrations.wolfram.com/CylindricalCoordinates/ Applet: Punkt in Zylinderkoordinaten (engl./ free CDF-Player erforderlich) http://www.pha.jhu.edu/~javalab/cylindrical/cylindrical.html Applet: Punkt in Zylinderkoordinaten (engl.) |
Hilfreiche Links
|
http://scientificsentence.net/Electromagnetics/index.php?key=yes&Integer=Cylindrical Bild und Erläuterung zu den Einheitsvektoren im Zylinderkoordinatensystem (engl.) http://www.math.wpi.edu/Course_Materials/MA2251C99/images/cylndrcl.gif Bild zu infinitesimalen Volumenelement in Zylinderkoordinatensystem http://lh5.ggpht.com/_XvrTyMj5b-k/SaH0PTc-qWI/AAAAAAAAFnM/YYo0W-gT_5I/controlvolumecylindricalcontinuity5.png Bild zu einem infinitesimalen Volumenelement in Zylinderkoordinaten |
| ← Zurück: Das kartesische Koordinatensystem | Übersicht: Orthogonale Koordinatensysteme | Vorwärts: Kugelkoordinaten → |
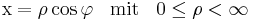
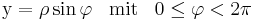
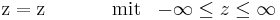
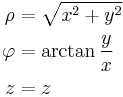
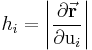
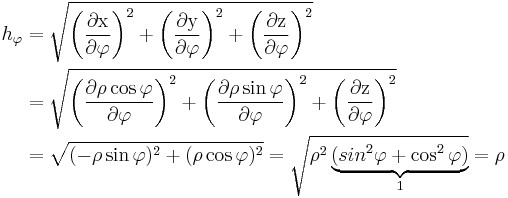
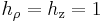
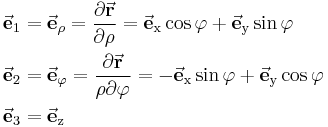
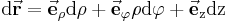
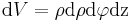
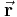 in kartesischen Koordinaten gegeben:
in kartesischen Koordinaten gegeben:

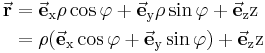
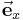 und
und 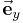 sich im zylindrischen System in dem Einheitsvektor
sich im zylindrischen System in dem Einheitsvektor 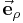 ausdrücken lassen:
ausdrücken lassen: