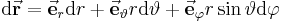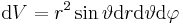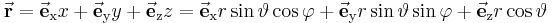Kugelkoordinaten: Unterschied zwischen den Versionen
(→Übersicht) |
(→Übersicht) |
||
| Zeile 76: | Zeile 76: | ||
|style="background-color:#c9d7ec"| <math>\vec{\textbf{e}}_3 = \vec{\textbf{e}}_\varphi = \frac{1}{r \sin\vartheta}\frac{\partial \vec{\textbf{r}}}{\partial \varphi} = | |style="background-color:#c9d7ec"| <math>\vec{\textbf{e}}_3 = \vec{\textbf{e}}_\varphi = \frac{1}{r \sin\vartheta}\frac{\partial \vec{\textbf{r}}}{\partial \varphi} = | ||
-\vec{\textbf{e}}_\mathrm{x} \sin\varphi + \vec{\textbf{e}}_\mathrm{y} \cos\varphi </math> | -\vec{\textbf{e}}_\mathrm{x} \sin\varphi + \vec{\textbf{e}}_\mathrm{y} \cos\varphi </math> | ||
| + | | rowspan="3" style="background-color:#dde6f3;" |Einheitsvektoren | ||
| + | | style="background-color:#c9d7ec"|<math>\vec{\textbf{e}}_1 = \vec{\textbf{e}}_r = \frac{\partial \vec{\textbf{r}}}{\partial r} =\vec{\textbf{e}}_\mathrm{x} \sin\vartheta \cos\varphi + \vec{\textbf{e}}_\mathrm{y} \sin\vartheta \sin\varphi + \vec{\textbf{e}}_\mathrm{z} \cos\vartheta </math> | ||
| + | |- | ||
| + | |style="background-color:#c9d7ec"| <math>\vec{\textbf{e}}_2 = \vec{\textbf{e}}_\vartheta = \frac{1}{r}\frac{\partial \vec{\textbf{r}}}{\partial \vartheta} =\vec{\textbf{e}}_\mathrm{x} \cos\vartheta \cos\varphi + \vec{\textbf{e}}_\mathrm{y} \cos\vartheta \sin\varphi - \vec{\textbf{e}}_\mathrm{z} \sin\vartheta </math> | ||
| + | |- | ||
| + | |style="background-color:#c9d7ec"| <math>\vec{\textbf{e}}_3 = \vec{\textbf{e}}_\varphi = \frac{1}{r \sin\vartheta}\frac{\partial \vec{\textbf{r}}}{\partial \varphi} = | ||
| + | -\vec{\textbf{e}}_\mathrm{x} \sin\varphi + \vec{\textbf{e}}_\mathrm{y} \cos\varphi </math> | ||
| + | |||
|} | |} | ||
Version vom 5. April 2012, 14:37 Uhr
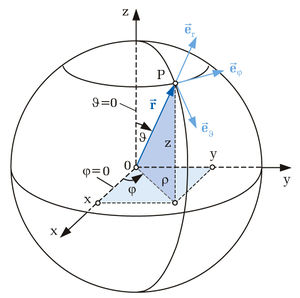
Bei den Kugelkoordinaten  beschreibt die Koordinate
beschreibt die Koordinate 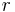 den Abstand eines Punktes
den Abstand eines Punktes 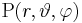 vom Ursprung. Die Koordinatenfläche
vom Ursprung. Die Koordinatenfläche 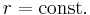 entspricht einer konzentrisch um den Ursprung liegenden Kugelfläche. Der Winkel
entspricht einer konzentrisch um den Ursprung liegenden Kugelfläche. Der Winkel 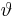 wird von der positiven z-Achse und dem Ursprung zum Punkt P zeigenden Ortsvektor eingeschlossen. Er wird definitionsgemäß beginnend bei der positiven z-Achse gezählt und durchläuft den Wertebereich
wird von der positiven z-Achse und dem Ursprung zum Punkt P zeigenden Ortsvektor eingeschlossen. Er wird definitionsgemäß beginnend bei der positiven z-Achse gezählt und durchläuft den Wertebereich 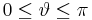 . Der positiven z-Achse ist der Wert
. Der positiven z-Achse ist der Wert 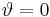 zugeordnet, der negativen z-Achse der Wert
zugeordnet, der negativen z-Achse der Wert 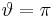 . Alle Punkte auf der Kugel mit gleichen
. Alle Punkte auf der Kugel mit gleichen 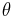 liegen auf einem Breitenkreis, z. B. gilt für alle Punkte auf dem Äquator
liegen auf einem Breitenkreis, z. B. gilt für alle Punkte auf dem Äquator 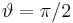 . Die Koordinate
. Die Koordinate  ist identisch mit der entsprechenden Koordinate im Zylinderkoordinatensystem.
ist identisch mit der entsprechenden Koordinate im Zylinderkoordinatensystem.
Ein Punkt 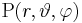 auf der Kugeloberfläche hat die z-Koordinate
auf der Kugeloberfläche hat die z-Koordinate 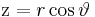 und den Abstand
und den Abstand 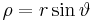 von der z-Achse. Setzt man diesen Abstand , dann stellt man fest, dass die Kugelkoordinaten mit den kartesischen Koordinaten über die Definitionsgleichungen in der Form:
von der z-Achse. Setzt man diesen Abstand , dann stellt man fest, dass die Kugelkoordinaten mit den kartesischen Koordinaten über die Definitionsgleichungen in der Form:
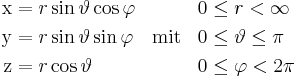
verknüpft sind. Die metrischen Faktoren können durch Einsetzen der Definitionsgleichungen berechnet werden:
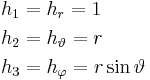
und den metrischen Faktoren die Einheitsvektoren bestimmt:
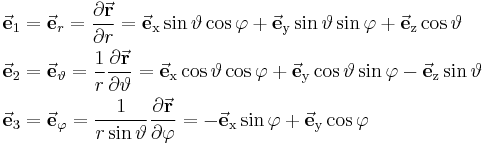
Für das vektorielle Wegelement folgt unmittelbar mit
und für das Volumenelement:
Mit dem Ortsvektor
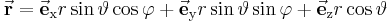
Übersicht
| Einheitsvektoren | 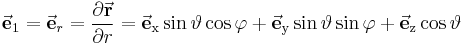
| |
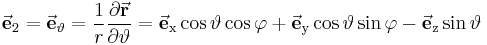
| ||
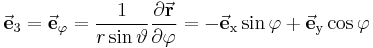
|
Einheitsvektoren | 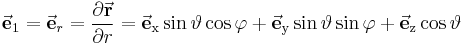
|
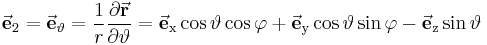
| ||
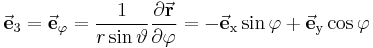
|
Bei den Zylinderkoordinaten wurde schon gezeigt, dass sich der Ortsvektor vereinfachter darstellen lässt. Berechnet man den Ortsvektor in Kugelkoordinaten wird die Darstellung noch simpler: Zunächst wird die allgemeine Gleichung vom Ortsvektor benutzt und die obigen Transformationsgleichungen eingesetzt: Durch hervorziehen des Faktors r und vergleich mit den Einheitsvektoren der Kugelkoordinaten erkennt man direkt den einfachen Zusammenhang für den Ortsvektor in Kugelkoordinaten: |
Multimediale Lehrmaterialien
|
http://demonstrations.wolfram.com/ExploringSphericalCoordinates/ Applet: Punkt in Polarkoordinaten (engl./ free CDF-Player von Wolfram erforderlich) http://www.pha.jhu.edu/~javalab/spherical/spherical.html Applet: Punkt in Polarkoordinaten (engl.) http://demonstrations.wolfram.com/SphericalCoordinates/ Applet: Punkt in Polarkoordinaten (engl. / free CDF-Player erforderlich) |
Hilfreiche Links
|
http://de.academic.ru/pictures/dewiki/83/Sphere_3d.png dreidimensionales Bild zur Bestimmung eines Punktes in Kugelkoordinaten http://mathworld.wolfram.com/PolarCoordinates.html Allgemeine Einführung in die Polarkoordinaten (engl.) |
| ← Zurück: Zylinderkoordinaten | Übersicht: Orthogonale Koordinatensysteme | Vorwärts: Orthogonale Koordinatensysteme:Übersicht → |