Zylinderkoordinaten: Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
| − | Um Zylinderkoordinaten zu verstehen, hilft es sich einen Zylinder vorzustellen und ihn in seine Bestandteile, also Deckel und Mantelflächen zu unterteilen. Die Deckelfläche lässt sich dabei am einfachsten mit ihren Radius <math>\rho</math> und dem Winkel <math>\varphi</math> beschreiben. | + | Um Zylinderkoordinaten zu verstehen, hilft es sich einen Zylinder vorzustellen und ihn in seine Bestandteile, also Deckel und Mantelflächen zu unterteilen. Die Deckelfläche lässt sich dabei am einfachsten mit ihren Radius <math>\rho</math> und dem Winkel <math>\varphi</math> beschreiben, dabei wird der Winkel <math>\varphi</math> definitionsgemäß beginnend bei der positiven x-Achse entgegen dem Uhrzeigersinn gezählt. Um auch noch die Höhe berücksichtigen zu können wählt man die z-Koordinate, die schon aus den kartesichen Koordinaten bekannt ist. Diese entspricht der Länge der Mantelfläche des Zylinders. Mit diesen drei Koordinaten lässt sich jeder Raumpunkt erfassen. Dabei können Sie folgende Werte annehmen: |
| − | + | :<math>0\leq \rho\leq\infty</math> | |
| + | :<math>0\leq \varphi\leq 2\pi</math> | ||
| + | :<math>-\infty\leq z\leq\infty</math> | ||
| − | + | <figure id="fig:krummlinige_koordinaten3"> | |
| + | [[Image:Koordinatensysteme_Krummlinige_Koordinaten3.jpg|miniatur|<caption>Zylinderkoordinaten</caption>]] | ||
| + | </figure> | ||
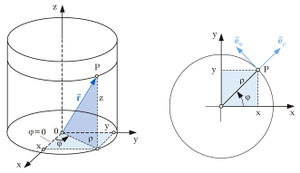
| − | + | Die Definitionsgleichungen <xr id="eqn:definition"/> für die Koordinaten des Kreiszylinders <math>\left( \mathrm{u}_1 = \rho, \mathrm{u}_2 = \varphi, \mathrm{u}_3 = \mathrm{z} \right)</math> können unmittelbar der unteren Abbildung entnommen werden: | |
:<equation id="eqn:definition2"> | :<equation id="eqn:definition2"> | ||
<math> | <math> | ||
| Zeile 23: | Zeile 27: | ||
<xr id="eqn:definition2" /> | <xr id="eqn:definition2" /> | ||
| − | + | ||
| − | |||
| − | |||
Die metrischen Faktoren können durch Einsetzen der Definitionsgleichungen <xr id="eqn:definition2"/> in die <xr id="eqn:metrisch"/> berechnet werden: | Die metrischen Faktoren können durch Einsetzen der Definitionsgleichungen <xr id="eqn:definition2"/> in die <xr id="eqn:metrisch"/> berechnet werden: | ||
:<equation id="eqn:faktoren"> | :<equation id="eqn:faktoren"> | ||
Version vom 3. April 2012, 14:35 Uhr
Um Zylinderkoordinaten zu verstehen, hilft es sich einen Zylinder vorzustellen und ihn in seine Bestandteile, also Deckel und Mantelflächen zu unterteilen. Die Deckelfläche lässt sich dabei am einfachsten mit ihren Radius 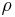 und dem Winkel
und dem Winkel  beschreiben, dabei wird der Winkel
beschreiben, dabei wird der Winkel  definitionsgemäß beginnend bei der positiven x-Achse entgegen dem Uhrzeigersinn gezählt. Um auch noch die Höhe berücksichtigen zu können wählt man die z-Koordinate, die schon aus den kartesichen Koordinaten bekannt ist. Diese entspricht der Länge der Mantelfläche des Zylinders. Mit diesen drei Koordinaten lässt sich jeder Raumpunkt erfassen. Dabei können Sie folgende Werte annehmen:
definitionsgemäß beginnend bei der positiven x-Achse entgegen dem Uhrzeigersinn gezählt. Um auch noch die Höhe berücksichtigen zu können wählt man die z-Koordinate, die schon aus den kartesichen Koordinaten bekannt ist. Diese entspricht der Länge der Mantelfläche des Zylinders. Mit diesen drei Koordinaten lässt sich jeder Raumpunkt erfassen. Dabei können Sie folgende Werte annehmen:
Die Definitionsgleichungen ??? für die Koordinaten des Kreiszylinders 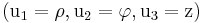 können unmittelbar der unteren Abbildung entnommen werden:
können unmittelbar der unteren Abbildung entnommen werden:
Formel (1)
Die metrischen Faktoren können durch Einsetzen der Definitionsgleichungen Formel (1) in die ??? berechnet werden:
Formel (2)
Für das vektorielle Wegelement folgt unmittelbar mit ???:
Für das Volumenelement folgt mit ???:
Mit dem Ortsvektor (???)
Formel (3)
und den metrischen Faktoren (Formel (2)) werden aus ??? die Einheitsvektoren bestimmt:
Formel (4)
Ein Vergleich der Beziehungen Formel (3) und Formel (4) zeigt, dass der Ortsvektor in Zylinderkoordinaten die nachstehende Form annimmt:
Gegeben sei der Ortsvektor Nun soll man diesen Vektor in zylindrischen Koordinaten ausdrücken: |
Multimediale Lehrmaterialien
|
http://demonstrations.wolfram.com/ExploringCylindricalCoordinates/ Applet: Punkt in Zylinderkoordinaten (engl./ free CDF-Player erforderlich) http://demonstrations.wolfram.com/CylindricalCoordinates/ Applet: Punkt in Zylinderkoordinaten (engl./ free CDF-Player erforderlich) http://www.pha.jhu.edu/~javalab/cylindrical/cylindrical.html Applet: Punkt in Zylinderkoordinaten (engl.) |
Hilfreiche Links
|
http://scientificsentence.net/Electromagnetics/index.php?key=yes&Integer=Cylindrical Bild und Erläuterung zu den Einheitsvektoren im Zylinderkoordinatensystem (engl.) http://www.math.wpi.edu/Course_Materials/MA2251C99/images/cylndrcl.gif Bild zu infinitesimalen Volumenelement in Zylinderkoordinatensystem http://lh5.ggpht.com/_XvrTyMj5b-k/SaH0PTc-qWI/AAAAAAAAFnM/YYo0W-gT_5I/controlvolumecylindricalcontinuity5.png Bild zu einem infinitesimalen Volumenelement in Zylinderkoordinaten |
| ← Zurück: Krummlinige orthogonale Koordinatensysteme | Übersicht: Orthogonale Koordinatensysteme | Vorwärts: Kugelkoordinaten → |
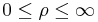
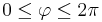
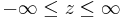
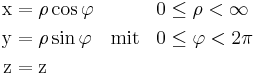
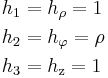
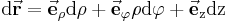
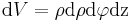
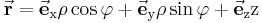
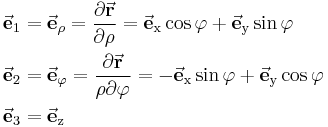
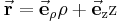
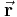 in kartesischen Koordinaten.
in kartesischen Koordinaten.


