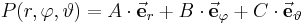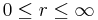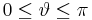Orthogonale Koordinatensysteme:Übersicht: Unterschied zwischen den Versionen
(→Übersicht) |
(→Übersicht) |
||
| Zeile 40: | Zeile 40: | ||
|style="background-color:#c9d7ec"| | |style="background-color:#c9d7ec"| | ||
:<math>P(u_1,u_2,u_3)=A\cdot\vec{\mathbf{e}}_1+B\cdot\vec{\mathbf{e}}_2+C\cdot\vec{\mathbf{e}}_3</math> | :<math>P(u_1,u_2,u_3)=A\cdot\vec{\mathbf{e}}_1+B\cdot\vec{\mathbf{e}}_2+C\cdot\vec{\mathbf{e}}_3</math> | ||
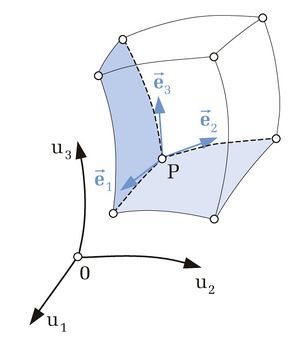
| − | |style="background-color:#dde6f3"|[[Image:Koordinatensysteme_Krummlinige_Koordinaten.jpg|miniatur| | + | |style="background-color:#dde6f3"|[[Image:Koordinatensysteme_Krummlinige_Koordinaten.jpg|miniatur|Krummlinige Koordinaten]] |
|- | |- | ||
| Zeile 50: | Zeile 50: | ||
:<math>0\leq \varphi\leq 2\pi</math> | :<math>0\leq \varphi\leq 2\pi</math> | ||
:<math>-\infty\leq z\leq\infty</math> | :<math>-\infty\leq z\leq\infty</math> | ||
| − | |style="background-color:#dde6f3"|[[Image:Koordinatensysteme_Krummlinige_Koordinaten3.jpg|miniatur| | + | |style="background-color:#dde6f3"|[[Image:Koordinatensysteme_Krummlinige_Koordinaten3.jpg|miniatur|Zylinderkoordinaten]] |
|- | |- | ||
|style="background-color:#dde6f3"|[[Kugelkoordinaten]] | |style="background-color:#dde6f3"|[[Kugelkoordinaten]] | ||
| Zeile 59: | Zeile 59: | ||
:<math>0\leq \varphi\leq 2\pi</math> | :<math>0\leq \varphi\leq 2\pi</math> | ||
:<math>0\leq \vartheta\leq\pi</math> | :<math>0\leq \vartheta\leq\pi</math> | ||
| − | |style="background-color:#dde6f3"|[[Image:Koordinatensysteme_Krummlinige_Koordinaten4.jpg|miniatur| | + | |style="background-color:#dde6f3"|[[Image:Koordinatensysteme_Krummlinige_Koordinaten4.jpg|miniatur|Kugelkoordinaten]] |
|} | |} | ||
Version vom 20. März 2012, 18:44 Uhr
Einführung
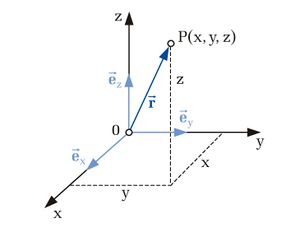
Die Position eines Punktes P im dreidimensionalen Raum bezogen auf einen anderen willkürlich gewählten Bezugspunkt Q kann mithilfe eines von Q nach P zeigenden Vektors eindeutig gekennzeichnet werden. Eine vollständige mathematische Beschreibung dieses Vektors kann durch die Angabe der Koordinaten von Anfangspunkt Q und Endpunkt P erfolgen. Unter den Koordinaten eines Punktes versteht man Zahlenwerte zur Festlegung seiner Position im Raum. Alternativ zu diesen Koordinaten kann der Vektor auch durch die Angabe seiner drei Komponenten eindeutig beschrieben werden. Diese werden üblicherweise so gewählt, dass sie senkrecht aufeinander stehen, man spricht dann davon, dass diese Komponenten zueinander orthogonal sind.
Sowohl zur Angabe der Koordinatenwerte als auch bei der Zerlegung des Vektors in seine Komponenten bedient man sich der Koordinatensysteme. Es erweist sich in der Praxis als sehr zweckmäßig, ein der jeweiligen Problemstellung angepasstes Koordinatensystem zu verwenden. Bei den in den folgenden Abschnitten betrachteten drei Fällen, nämlich den kartesischen Koordinaten, den Zylinderkoordinaten und den Kugelkoordinaten handelt es sich um orthogonale Rechtssysteme, d. h. die in Richtung wachsender Koordinatenwerte weisenden Einheitsvektoren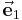 
, 
, 
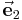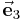stehen senkrecht aufeinander und erfüllen somit die Bedingung der Orthogonalität:
Formel (1)
Bei einem Rechtssystem liefert das Vektorprodukt zweier aufeinander folgender Einheitsvektoren den jeweils nächsten Einheitsvektor, so dass die nachstehenden Gleichungen gelten:
Formel (2)
Übersicht
| Das kartesische Koordinatensystem
Bei dem kartesischen Koordinatensystem sind die Koordinatenachsen geradlinig und orthogonal angeordnet, so dass die Achsen ein Rechtssystem bilden, welches durch die Rechte Handregel1 beschrieben werden kann. Der Schnittpunkt der Achsen wird Koordinatenursprung genannt. Die Einheitsvektoren sind parallel zu den Achsen angeordnet und zeigen immer in Richtung wachsender Koordinatenwerte, daher sind die Einheitsvektoren auch unabhängig von der Position im Raum und zeigen immer dieselbe Richtung an. |
|
|
| Krummlinige orthogonale Koordinatensysteme |
|
|
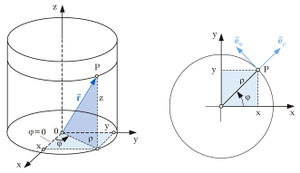
| Zylinderkoordinaten
Bei den Zylinderkoordinaten bleibt die z Koordinate im Vergleich zu den kartesischen Koordinaten unverändert. In der xy-Ebene werden allerdings |
|
|
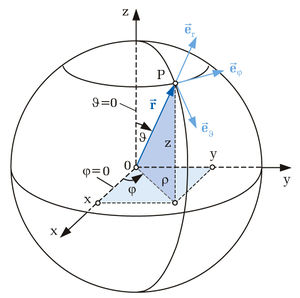
| Kugelkoordinaten
Bei dem Kugelkoordinatensystem bestimmt r den Abstand zum Ursprung. |
|
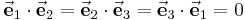
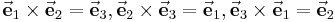
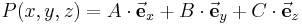
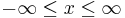
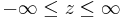
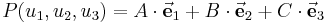
und 
verwendet. 
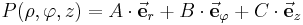
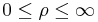
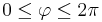
, er wird zwischen der positiven z-Achse und dem Punkt P gemessen. Auch hier gilt, alle Punkte mit dem selben Winkel 
