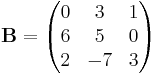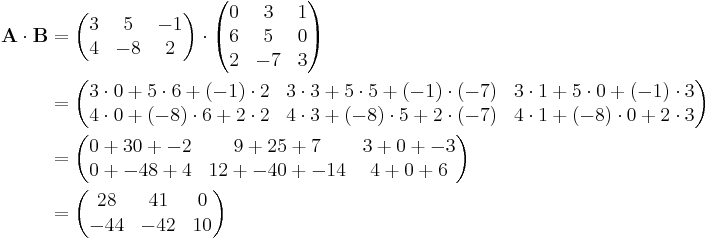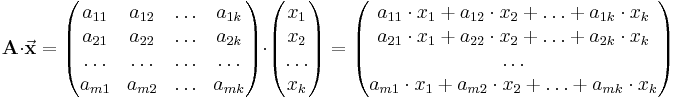Multiplikation von Matrizen
|
Dieser Artikel befindet sich noch im Aufbau. |
| ← Zurück: Komponenten des linearen Gleichungssystems | Übersicht: Lineare Gleichungssysteme | Vorwärts: Inverse einer Matrix & Einheitsmatrix → |
Multiplikation zweier Matrizen
Bei der Berechnung von linearen Gleichungssystemen kann es vorkommen, dass man zwei verschiedene Matrizen erhält, die man miteinander multiplizieren muss, um die gesamt Matrix zu erhalten. Da die Rechenregeln von Matrizenrechnungen nicht immer denen von skalaren Operationen entspricht, soll hier zunächst eine der wichtigsten Operationen besprochen werden, die Matrizenmultiplikation.
Möchte man zwei Matrizen multiplizieren, gibt es ein bestimmtes Rechenschema, dass eingehalten werden muss. Dabei ist es wichtig, dass die Zeilenanzahl der ersten Matrix mit der Spaltenanzahl der zweiten Matrix übereinstimmt. Dies impliziert auch, dass die Matrizenmultiplikation nicht kommuntativ ist, also die Matrizen in einer Rechnung auf keinen Fall getauscht werden dürfen.
Um nun das erste Element der neuen Matrix zu berechnen, muss man das erste Element der ersten Zeile der ersten Matrix mit dem ersten Element der ersten Spalte der zweiten Matrix multiplizieren und anschließend das zweite Element der ersten Zeile der ersten Matrix mit dem zweiten Element der ersten Spalte der zweiten Matrix multipliziert und die Ergebnisse der Multiplikationen aufaddiert werden. Dies führt man solange durch, bis das letzte Element der ersten Zeile der ersten Matrix und das letzte Element der ersten Spalte der zweiten Matrix erreicht ist. Daraus folgt auch, die Gleichheit der Zeilenanzahl der ersten Matrix mit der Spaltenanzahl der zweiten Matrix, die vorher schon gefordert wurde.
Einfacher wird es wenn man sich zwei kleine Matrizen, als Beispiel 2 2x2-Matrizen anschaut. Dort lautet das Rechenschema:
Eine weitere Merkhilfe bietet das, in der Abbildung an einer 2x2-Matrix gezeigte Falk-Schema. Hier wird die Matrix A links von der zu berechnenden Matrix aufgetragen und die Matrix B über der zu berechnenden Matrix eingezeichnet. Um ein Element in der gesuchten Matrix zu erhalten, betrachtet man nun die Elemente, die bei der Matrix A in der selben Zeile stehen und bei der Matrix B in der selben Spalte, also entlang der eingezeichneten Linien. Nun muss man nur noch das Skalarprodukt aus dem Zeilenvektor von der Matrix A und dem Spaltenvektor aus der Matrix B gebildet werden, um das Element zu berechnen.
In diesem Beispiel sind die zwei Matrizen A und B gegeben:
Wie man sieht sind die beiden Matrizen A und B nicht gleich dimensioniert. Allerdings stimmt die Zeilenanzahl der ersten Matrix mit der Spaltenanzahl der zweiten Matrix überein. Also sind diese beiden Matrizen multiplizierbar. Als Formel kann man sich merken, dass das Produkt der Matrizen die selbe Spaltenanzahl, wie die erste Matrix und die selbe Zeilenanzahl, wie die zweite Matrix besitzen muss. Nutzt man nun die oben genannte Form ergibt sich: |
Multiplikation von Matrix und Vektor
Vektoren können als Sonderform von Matrizen betrachtet werden, die nur eine Spalte besitzen. Möchte man eine Matrix mit einen Vektor multiplizieren muss also immer zuerst die Matrix stehen und anschließend erst der Vektor und die Zeilenanzahl der Matrix muss der Spaltenanzahl des Vektors entsprechen:

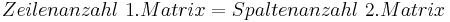
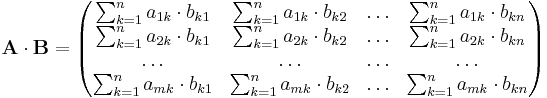
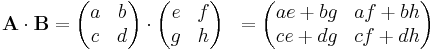
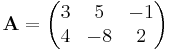 und
und