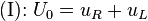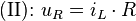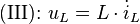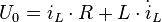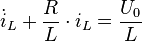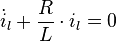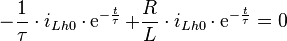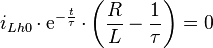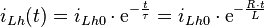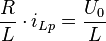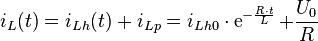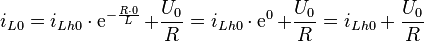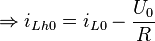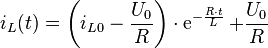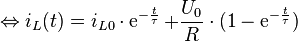Getb:Beispiel für eine DGL 1. Ordnung: Das RL-Glied
| ← Zurück: Getb:Differenzialgleichungen bei elektrischen Netzwerken | Übersicht: Beispiel für eine DGL 1. Ordnung: Das RL-Glied | Vorwärts: Getb:Beispiel für eine DGL 2. Ordnung: Ein RLC-Schwingkreis → |
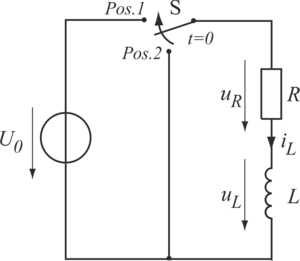
Zum Zeitpunkt 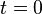 wird der Schalter S der nebenstehenden Schaltung von Position 2 auf Position 1 umgelegt. Gesucht ist der Verlauf des Stroms
wird der Schalter S der nebenstehenden Schaltung von Position 2 auf Position 1 umgelegt. Gesucht ist der Verlauf des Stroms 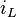 , also die Funktion
, also die Funktion 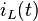 für
für 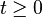 .
.
Inhaltsverzeichnis
Aufstellen der Differenzialgleichung
Um die Funktion 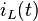 zu finden, werden die Maschengleichung und die Zweipolgleichungen ausgewertet:
zu finden, werden die Maschengleichung und die Zweipolgleichungen ausgewertet:
Werden nun Gleichung (II) und Gleichung (III) in (I) eingesetzt, erhält man eine DGL 1. Ordnung:
Dass diese DGL linear ist, sieht man, wenn man die gesamte Gleichung durch 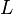 teilt und damit auf die allgemeine Form einer linearen DGL bringt:
teilt und damit auf die allgemeine Form einer linearen DGL bringt:
Es liegt also eine lineare Differenzialgleichung 1. Ordnung vor. Diese Gleichung beschreibt nicht den zeitlichen Verlauf des Stroms 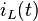 , sondern setzt die zeitliche Änderung (Ableitung) des Stroms
, sondern setzt die zeitliche Änderung (Ableitung) des Stroms 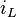 ins Verhältnis zu seinem momentanen Wert und der Eingangsspannung
ins Verhältnis zu seinem momentanen Wert und der Eingangsspannung 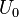 . Die Lösung dieser DGL ist die gesuchte Funktion
. Die Lösung dieser DGL ist die gesuchte Funktion 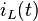 , die den Stromverlauf beschreibt. Dieser Stromverlauf entspricht den Zusammenhängen der DGL und muss auch den noch zu betrachtenden Anfangsbedingungen entsprechen.
, die den Stromverlauf beschreibt. Dieser Stromverlauf entspricht den Zusammenhängen der DGL und muss auch den noch zu betrachtenden Anfangsbedingungen entsprechen.
Lösung der homogenen Differenzialgleichung
Ziel ist es, die eben aufgestellte DGL für das RL-Glied zu lösen. Die dazugehörige homogene DGL lautet:
Die gesuchte Funktion ist der Verlauf des Stroms 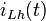 . Zur Lösung wird der Exponentialansatz angesetzt. Der gesuchte Strom
. Zur Lösung wird der Exponentialansatz angesetzt. Der gesuchte Strom 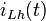 hat die Einheit Ampere, sodass auch die Konstante
hat die Einheit Ampere, sodass auch die Konstante  die Einheit Ampere hat, während die Exponentialfunktion einheitenlos ist. Statt mit
die Einheit Ampere hat, während die Exponentialfunktion einheitenlos ist. Statt mit 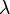 wird der Exponentialansatz mit
wird der Exponentialansatz mit 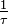 geschrieben, um den Zusammenhang mit der Zeitkonstante
geschrieben, um den Zusammenhang mit der Zeitkonstante 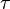 der Schaltung zu verdeutlichen. Der Exponentialansatz und dessen Ableitung lauten für diesen Fall also:
der Schaltung zu verdeutlichen. Der Exponentialansatz und dessen Ableitung lauten für diesen Fall also:
Beides kann nun in die homogene DGL eingesetzt werden. Es ergibt sich:
Zusammenfassen liefert folgenden Ausdruck:
Diese Gleichung ist erfüllt, wenn einer der Faktoren gleich 0 ist. Die e-Funktion kann niemals null sein. Der Fall 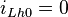 führt zur Lösung
führt zur Lösung 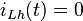 und ist für die Praxis meist nicht relevant, da sich in diesem Fall der Strom
und ist für die Praxis meist nicht relevant, da sich in diesem Fall der Strom 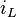 nicht zeitlich ändern würde. Aus
nicht zeitlich ändern würde. Aus 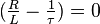 folgt aber
folgt aber 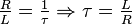 . Damit wurde die Zeitkonstante der Schaltung bestimmt und die Lösung für die homogene DGL lautet:
. Damit wurde die Zeitkonstante der Schaltung bestimmt und die Lösung für die homogene DGL lautet:
Lösung der inhomogenen Differenzialgleichung
Gesucht wird eine partikuläre Lösung 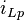 der inhomogenen DGL
der inhomogenen DGL
Da die rechte Seite mit 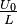 konstant ist, kann für
konstant ist, kann für 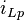 auch ein konstanter Wert angenommen werden. Dann gilt
auch ein konstanter Wert angenommen werden. Dann gilt 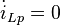 und die Gleichung vereinfacht sich zu:
und die Gleichung vereinfacht sich zu:
Durch Umstellen sieht man, dass 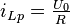 eine partikuläre Lösung der inhomogenen DGL ist. Die allgemeine Lösung der inhomogenen DGL lautet also:
eine partikuläre Lösung der inhomogenen DGL ist. Die allgemeine Lösung der inhomogenen DGL lautet also:
Anpassung der allgemeinen Lösung an die spezielle Anwendung
In der vorherigen Rechnung wurde für den Strom 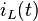 die allgemeine Lösung gefunden. Dabei ist die Größe
die allgemeine Lösung gefunden. Dabei ist die Größe  noch unbestimmt. Aus dem Strom
noch unbestimmt. Aus dem Strom 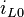 , der zum Zeitpunkt
, der zum Zeitpunkt 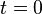 durch die Spule fließt, resultiert die Anfangsbedingung
durch die Spule fließt, resultiert die Anfangsbedingung 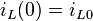 . Einsetzen in die allgemeine Lösung liefert:
. Einsetzen in die allgemeine Lösung liefert:
Damit kann nun die endgültige Lösung für den Strom 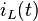 bestimmt werden:
bestimmt werden:
In der zweiten Darstellung wurde lediglich die schon bestimmte Zeitkonstante 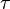 verwendet und die Gleichung etwas anders zusammengefasst.
verwendet und die Gleichung etwas anders zusammengefasst.