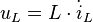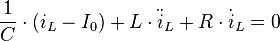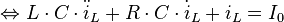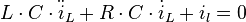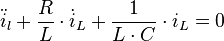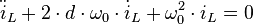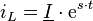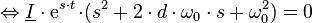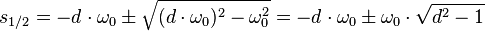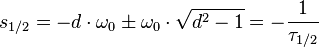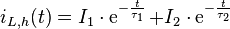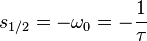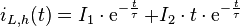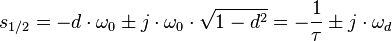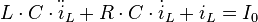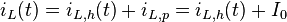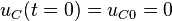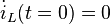Getb:Beispiel für eine DGL 2. Ordnung: Ein RLC-Schwingkreis

← Zurück: Getb:Beispiel für eine DGL 1. Ordnung: Das RL-Glied

Übersicht: Beispiel für eine DGL 2. Ordnung: Ein RLC-Schwingkreis

Vorwärts: Getb:Hauptseite →

RLC-Schaltung

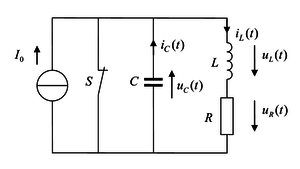
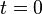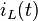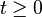Zum Zeitpunk $t=0$ wird der Schalter S der nebenstehenden Schaltung geöffnet. Ziel ist es, den Strom $i_L (t)$ für $t \ge 0$ zu bestimmen.

Aufstellen der Differenzialgleichung

Als Vorbereitung können zuerst die Bauteilgleichungen ausgewertet werden:

$u_R = i_L \cdot R$

$u_L = L \cdot \dot i_L$

$i_C = C \cdot \dot u_C \Leftrightarrow \dot u_C = \frac{1}{C} \cdot i_C$

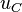Des Weiteren gilt die Maschengleichung $u_C + u_L + u_R = 0$. Da $u_C$ in der Bauteilgleichung nur in der ersten Ableitung vorkommt, ist es vorteilhaft, die Zeitableitung der Maschengleichung zu bilden, und dort alle drei Bauteilgleichungen direkt einzusetzen. Dazu müssen noch die Bauteilgleichung des Widerstands und der Spule abgeleitet werden:

$\dot u_C + \dot u_L + \dot u_R = 0 \Leftrightarrow \frac{1}{C} \cdot i_C + L \cdot \ddot i_L + R \cdot \dot i_L = 0$

Nun muss noch der Strom 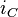$i_C$ durch den Strom 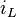$i_L$ ausgedrückt werden. Dies geschieht mit Hilfe der Knotengleichung $I_0 + i_C = i_L \Leftrightarrow i_C = i_L - I_0$:

$\frac{1}{C} \cdot (i_L - I_0) + L \cdot \ddot i_L + R \cdot \dot i_L = 0$

$\Leftrightarrow L \cdot C \cdot \ddot i_L + R \cdot C \cdot \dot i_L + i_L = I_0$

Es wurde also eine Differenzialgleichung 2. Ordnung mit konstanten Koeffizienten gefunden. Teilt man die Gleichung durch 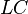$LC$, erhält man allgemeine Form einer linearen DGL 2. Ordnung. Diese Gleichung beschreibt nicht unmittelbar den Verlauf des Stroms 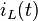$i_L (t)$, sondern nur den Zusammenhang zwischen dem momentanen Wert 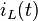$i_L (t)$, seinen zeitlichen Ableitungen, sowie den gegebenen Bauteilparametern 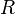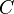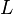$R$, $C$, $L$ und dem Quellstrom 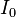$I_0$. Um den zeitlichen Verlauf des Stroms 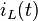$i_L (t)$ zu bestimmen, ist eine Lösung der DGL erforderlich.

Lösung der homogenen DGL

Die zur schaltung dazugehörige homogene DGL lautet:

$L \cdot C \cdot \ddot i_L + R \cdot C \cdot \dot i_L + i_l = 0$

Teilen durch 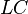$LC$ liefert folgende Form:

$\ddot i_l + \frac{R}{L} \cdot \dot i_L + \frac{1}{L \cdot C} \cdot i_L = 0$

Nun werden einige wichtige Abkürzungen eingeführt:

• Kennkreisfrequenz: $\textstyle \omega_0 = \frac{1}{\sqrt{L \cdot C}}$

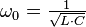
• Kennwiderstand: $\textstyle Z_0 = \sqrt{\frac{L}{C}}$

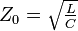
• Dämpfung: $\textstyle d = \frac{R}{2} \cdot \sqrt{\frac{C}{L}} = \frac{1}{2} \cdot \frac{R}{Z_0}$

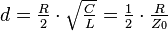
Damit lässt sich die homogene DGL kompakter darstellen:

$\ddot i_L + 2 \cdot d \cdot \omega_0 \cdot \dot i_L + \omega_{0}^2 \cdot i_L = 0$

Der Exponentialansatz lautet:

$i_L = \underline{I} \cdot \operatorname{e}^{s \cdot t}$

Es ist zu beachten, dass die möglicherweise komplexe Exponentialfunktion einheitenlos ist, und für die komplexe Konstante (sowohl Real- als auch Imaginärteil) $[\underline{I}]=A$ gilt, da für die Einheit des Spulenstroms $[i_L] = A$ gelten muss.

Einsetzen des Ansatzes liefert die charakteristische Gleichung:

$s^2 \cdot \underline{I} \cdot \operatorname{e}^{s \cdot t} + 2 \cdot d \cdot \omega_0 \cdot s \cdot \underline{I} \cdot \operatorname{e}^{s \cdot t} + \omega_{0}^2 \cdot \underline{I} \cdot \operatorname{e}^{s \cdot t} = 0$

$\Leftrightarrow \underline{I} \cdot \operatorname{e}^{s \cdot t} \cdot (s^2 + 2 \cdot d \cdot \omega_0 \cdot s + \omega_{0}^2 ) = 0$

$\Rightarrow s^2 + 2 \cdot d \cdot \omega_0 \cdot s + \omega_{0}^2 = 0$

Die Koeffizienten der charakteristischen Gleichung sind also identisch mit den Koeffizienten der homogenen DGL, wenn diese von der normalisierten Form einer linearen DGL ist. Die Lösung der charakteristischen Gleichung ergibt die Eigenwerte:

$s_{1/2} = -d \cdot \omega_0 \pm \sqrt{(d \cdot \omega_0)^2 - \omega_{0}^2} = -d \cdot \omega_0 \pm \omega_0 \cdot \sqrt{d^2 -1}$

Dies führt zu den drei verschiedenen Lösungsfällen:

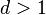1. $d > 1$ (starke Dämpfung) 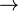$\rightarrow$ zwei verschiedene, reelle Eigenwerte
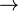2. $d = 1$ (aperiodischer Grenzfall) $\rightarrow$ zwei gleiche, reelle Eigenwerte
3. $d < 1$ (schwache Dämpfung) $\rightarrow$ zwei zueinander konjugiert komplexe Eigenwerte

Fall 1 (aperiodischer Fall):

Mit 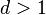$d > 1$ gilt für die Eigenwerte:

$s_{1/2} = -d \cdot \omega_0 \pm \omega_0 \cdot \sqrt{d^2 -1} = - \frac{1}{\tau_{1/2}}$

Damit ergibt sich die allgemeine Lösung:

$i_{L,h}(t) = I_1 \cdot \operatorname{e}^{- \frac{t}{\tau_1}} + I_2 \cdot \operatorname{e}^{- \frac{t}{\tau_2}}$

Da die e-Funktion einheitenlos ist, gilt hier für die Einheiten der Konstanten: $[I_1] = A$ und $[I_2]=A$.

Fall 2 (aperiodischer Grenzfall):

Mit $d=1$ gilt für die gleichen, reellen Eigenwerte:

$s_{1/2} = - \omega_0 = - \frac{1}{\tau}$

Damit ergibt sich die allgemeine Lösung:

$i_{L,h}(t) = I_1 \cdot \operatorname{e}^{- \frac{t}{\tau}} + I_2 \cdot t \cdot \operatorname{e}^{- \frac{t}{\tau}}$

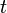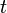Die e-Funktion ist einheitenlos und die Einheit der Zeit $t$ ist Sekunde. Deshalb muss für die Einheiten der Konstanten gelten: $[I_1] = A$ und $[I_2] = \frac{A}{s}$. Aufgrund der Multiplikation der zweiten Lösung mit der Zeit $t$ haben die Konstanten hier unterschiedliche Einheiten. Dies ist notwendig, da für den Spulenstrom $[i_{L,h}] = A$ gelten muss.

Fall 3 (Schwingfall):

Mit $d < 1$ gilt für die Eigenwerte:

$s_{1/2} = -d \cdot \omega_0 \pm j \cdot \omega_0 \cdot \sqrt{1 - d^2} = - \frac{1}{\tau} \pm j \cdot \omega_d$

Mit $\textstyle \tau = \frac{1}{\omega_{0} \cdot d}$ und der Eigenkreisfrequenz $\omega_d = \omega_0 \cdot \sqrt{1 - d^2}$.

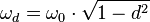Damit ergibt sich für 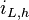$i_{L,h}$ die allgemeine Lösung:

$i_{L,h}(t) = \operatorname{e}^{- \frac{t}{\tau}} \cdot (I_1 \cdot \cos (\omega_d \cdot t) + I_2 \cdot \sin (\omega_d \cdot t))$

Die e-Funktion, der Kosinus und auch der Sinus sind einheitenlose Funktionen. Deshalb muss hier für die Einheiten der Konstanten gelten: $[I_1 ]=A$ und $[I_2 ]=A$.

Lösung der inhomogenen DGL

Gesucht wird eine partikuläre Lösung der inhomogenen DGL

$L \cdot C \cdot \ddot i_L + R \cdot C \cdot \dot i_L + i_L = I_0$

Es liegen konstante Koeffizienten vor, und auch der Ausdruck auf der rechten Seite der Gleichung ist konstant. Es bietet sich also an, für 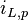$i_{L,p}$ einen konstanten Ausdruck anzunehmen. Man sieht, dass 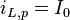$i_{L,p}=I_0$ eine partikuläre Lösung der DGL ist. Als allgemeine Lösung für die inhomogene DGL ergibt sich damit:

$i_L (t) = i_{L,h} (t) + i_{L,p} = i_{L,h} (t) + I_0$

Dabei ist 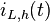$i_{L,h}(t)$ die Lösung der dazugehörigen homogenen DGL, die aus der vorherigen Fallunterscheidung hervorging.

Anpassung der allgemeinen Lösung an die spezielle Anwendung

Sollte in der oben angegebenen Schaltung der Schalter S für $t < 0$ lange genug geschlossen gewesen sein, wird in der Spule und in dem Kondensator keine Energie mehr gespeichert sein. Daraus ergeben sich die Anfangsbedingungen

$i_L (t=0) = i_{L0} = 0$

und

$u_C (t=0) = u_{C0} = 0$

Die Bedingung $i_L (t=0) = 0$ ist eine Anfangsbedingung für den Spulenstrom 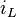$i_L$.

Die Bedingung 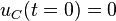$u_C (t=0) = 0$ erfordert dagegen eine weitere Betrachtung, um eine Anfangsbedingung für die zeitliche Ableitung des Spulenstroms 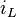$i_L$ zu erhalten. Unter Ausnutzung der Maschengleichung ergibt sich:

$u_C (0) = -u_R (0) - u_L (0) = -R \cdot i_L (0) - L \cdot \dot i_L (0) = -0 - L \cdot \dot i_L (0) = - L \cdot \dot i_L (0)$

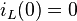wobei $i_L (0) = 0$ ausgenutzt wurde. Umgestellt auf die erste Ableitung des Stroms 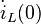$\dot i_L (0)$ ergibt sich die Anfangsbedingung:

$\dot i_L (0) = - \frac{u_C (0)}{L} = - \frac{u_{C0}}{L} = 0$

Damit wurden beide Anfangsbedingungen bestimmt:

$i_L (t=0) = 0$

$\dot i_L (t=0) = 0$

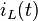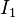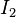Die beiden Anfangsbedingungen können nun in die allgemeine Lösung für den Spulenstrom $i_L (t)$, bzw. in dessen Ableitung, eingesetzt werden, um die beiden Konstanten $I_1$ und $I_2$ zu bestimmen.