Difference between revisions of "Multiplication of matrices"
| Line 78: | Line 78: | ||
|Contents= | |Contents= | ||
[[File:matrix_vector_mult.png|right|200px]] | [[File:matrix_vector_mult.png|right|200px]] | ||
| − | In chapter 3 of the robotics script some examples of matrices multiplied with vectors appear. On page 3-28 a transformation equation is presented for a rotation | + | In chapter 3 of the robotics script some examples of matrices multiplied with vectors appear. On page 3-28 a two-dimensional transformation equation is presented for a rotation about <math>\varphi</math> about the origin (see figure) in combination with a translation. The resulting vector is the following:<br/> |
| + | :<math> | ||
| + | \left[\begin{array}{c} | ||
| + | x_1 \\ | ||
| + | y_1 \\ | ||
| + | 1 | ||
| + | \end{array}\right]= | ||
| + | \left[\begin{array}{ccc} | ||
| + | \cos\varphi & -\sin\varphi & m\\ | ||
| + | \sin\varphi & \cos\varphi & n\\ | ||
| + | 0 & 0 & 1 | ||
| + | \end{array}\right] | ||
| + | \cdot | ||
| + | \left[\begin{array}{c} | ||
| + | x_0 \\ | ||
| + | y_0 \\ | ||
| + | 1 | ||
| + | \end{array}\right] = | ||
| + | \left[\begin{array}{c} | ||
| + | \cos\varphi\cdot x_0-\sin\varphi\cdot y_0+m\\ | ||
| + | \sin\varphi\cdot x_0+\cos\varphi\cdot y_0+n\\ | ||
| + | 0\cdot x_0+0\cdot y_0+1\cdot 1 | ||
| + | \end{array}\right]= | ||
| + | \left[\begin{array}{c} | ||
| + | \cos\varphi\cdot x_0-\sin\varphi\cdot y_0+m\\ | ||
| + | \sin\varphi\cdot x_0+\cos\varphi\cdot y_0+n\\ | ||
| + | 1 | ||
| + | \end{array}\right] | ||
| + | </math> | ||
}} | }} | ||
Revision as of 16:25, 16 May 2014
| ← Back: Addition of matrices | Overview: Matrices | Next: Matrix inversion → |
Two matrices can be multiplied if the number of colums of the left matrix equals the number of rows of the right matrix. The result of the multiplication of an l-by-m matrix 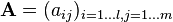 with an m-by-n matrix
with an m-by-n matrix 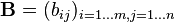 is an l-by-n matrix
is an l-by-n matrix 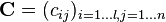 . The components of the resulting matrix are comuputed as follows:
. The components of the resulting matrix are comuputed as follows:
For example the multiplication of a 2-by-3 matrix with a 3-by-2 matrix results in a 2-by-2 matrix and is computed as follows:
Some further rules for matrix multiplications are:
A good example for the multiplication of several matrices in the context of robotics and transformations is presented in the robotics script. Please have a look in chapter 3 on page 3-35 |
Multiplication of matrices with vectors
A vector is a just special form of a matrix with either only one row or one column. Because an l-by-m matrix can only be multiplied by an m-by-n matrix, there are two possibilities of multiplying matrices and vectors. The first possibility is a 1-by-m row vector multiplied with an m-by-n matrix which results in a 1-by-n row vector:
The second possibility is a l-by-m matrix multiplied with an m-by-1 column vector which results in a l-by-1 column vector:
In chapter 3 of the robotics script some examples of matrices multiplied with vectors appear. On page 3-28 a two-dimensional transformation equation is presented for a rotation about |
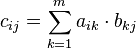
![\mathbf{A}\cdot\mathbf{B}=
\left[\begin{array}{ccc}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23}
\end{array}\right]\cdot
\left[\begin{array}{cc}
b_{11} & b_{12} \\
b_{21} & b_{22}\\
b_{31} & b_{32}
\end{array}\right]=
\left[\begin{array}{cc}
a_{11}\cdot b_{11}+a_{12}\cdot b_{21}+a_{13}\cdot b_{31} & a_{11}\cdot b_{12}+a_{12}\cdot b_{22}+a_{13}\cdot b_{12} \\
a_{21}\cdot b_{11}+a_{22}\cdot b_{21}+a_{23}\cdot b_{31} & a_{21}\cdot b_{12}+a_{22}\cdot b_{22}+a_{23}\cdot b_{12}
\end{array}\right]](/wiki/robotics/images/math/a/6/0/a60eb4b58962ac775002fcbe9dace286.png)
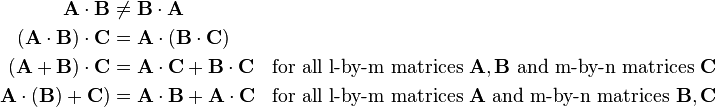
![\left[\begin{array}{ccc}
v_{11} & \dots & v_{1m}
\end{array}\right]
\cdot
\left[\begin{array}{ccc}
a_{11} & \dots & a_{1n}\\
\vdots & \ddots & \vdots\\
a_{m1} & \dots & a_{mn}
\end{array}\right]
=
\left[\begin{array}{ccc}
v_{11}a_{11}+\dots+v_{1m}a_{m1} & \dots & v_{11}a_{1n}+\dots+v_{1m}a_{mn}
\end{array}\right]](/wiki/robotics/images/math/1/9/7/197e995ca2b28be108faa7a88459bc18.png)
![\left[\begin{array}{ccc}
a_{11} & \dots & a_{1m}\\
\vdots & \ddots & \vdots\\
a_{l1} & \dots & a_{lm}
\end{array}\right]
\cdot
\left[\begin{array}{c}
v_{11}\\
\vdots \\
v_{m1}
\end{array}\right]
=
\left[\begin{array}{c}
a_{11}v_{11}+\dots+a_{1m}v_{m1}\\
\vdots \\
a_{l1}v_{11}+\dots+a_{lm}v_{m1}
\end{array}\right]](/wiki/robotics/images/math/8/5/d/85d25eb1c5233458e22b6f99c91978bc.png)
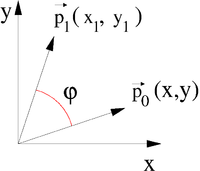
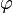 about the origin (see figure) in combination with a translation. The resulting vector is the following:
about the origin (see figure) in combination with a translation. The resulting vector is the following:![\left[\begin{array}{c}
x_1 \\
y_1 \\
1
\end{array}\right]=
\left[\begin{array}{ccc}
\cos\varphi & -\sin\varphi & m\\
\sin\varphi & \cos\varphi & n\\
0 & 0 & 1
\end{array}\right]
\cdot
\left[\begin{array}{c}
x_0 \\
y_0 \\
1
\end{array}\right] =
\left[\begin{array}{c}
\cos\varphi\cdot x_0-\sin\varphi\cdot y_0+m\\
\sin\varphi\cdot x_0+\cos\varphi\cdot y_0+n\\
0\cdot x_0+0\cdot y_0+1\cdot 1
\end{array}\right]=
\left[\begin{array}{c}
\cos\varphi\cdot x_0-\sin\varphi\cdot y_0+m\\
\sin\varphi\cdot x_0+\cos\varphi\cdot y_0+n\\
1
\end{array}\right]](/wiki/robotics/images/math/e/6/b/e6bebf6a1f6e5aead20a58c345e4f50c.png)