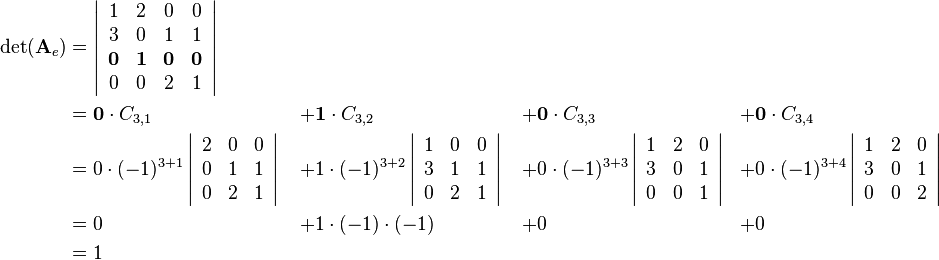Determinant of a matrix

This article describes a formula to compute the determinant of a 4-by-4 matrix using minors and cofactors of a matrix.

To compute the determinant of matrix 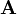$\mathbf{A}$ first one row or column is choosen. The sum of the four corresponding values of the row or column multiplied by the related cofactors results in the determinant:

$\det(\mathbf{A})=\sum_{(i,j) \isin \text{ one row or column}}{a_{i,j}C_{i,j}}$

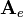Example: determinant of a 4-by-4 matrix $\mathbf{A}_e = \left[\begin{array}{cccc} 1 & 2 & 0 & 0\\ 3 & 0 & 1 & 1\\ 0 & 1 & 0 & 0\\ 0 & 0 & 2 & 1 \end{array}\right]$ For matrix $\mathbf{A}_e$ it is useful to choose row 3 because it contains three zero values as factors: $\begin{align} \det(\mathbf{A}_e)&= \left|\begin{array}{cccc} 1 & 2 & 0 & 0\\ 3 & 0 & 1 & 1\\ \mathbf{0} & \mathbf{1} & \mathbf{0} & \mathbf{0}\\ 0 & 0 & 2 & 1 \end{array}\right| & \quad & \quad & \quad\\ &= \mathbf{0}\cdot C_{3,1}&+&\mathbf{1}\cdot C_{3,2}&+&\mathbf{0}\cdot C_{3,3}&+&\mathbf{0}\cdot C_{3,4}\\ &= 0\cdot(-1)^{3+1} \left|\begin{array}{ccc} 2 & 0 & 0\\ 0 & 1 & 1\\ 0 & 2 & 1 \end{array}\right| &+&1\cdot(-1)^{3+2} \left|\begin{array}{ccc} 1 & 0 & 0\\ 3 & 1 & 1\\ 0 & 2 & 1 \end{array}\right| &+&0\cdot(-1)^{3+3} \left|\begin{array}{ccc} 1 & 2 & 0\\ 3 & 0 & 1\\ 0 & 0 & 1 \end{array}\right| &+&0\cdot(-1)^{3+4} \left|\begin{array}{ccc} 1 & 2 & 0\\ 3 & 0 & 1\\ 0 & 0 & 2 \end{array}\right|\\ &= 0&+&1\cdot(-1)\cdot(-1)&+&0&+&0\\ &= 1&\quad&\quad&\quad \end{align}$