Realization of transformations

← Back: Composition of rotations

Overview: Quaternions

Next: ??? →

Up to now transformations have been defined by homogeneous matrices combining a rotation matrix $\mathbf{R}$ and a translation vector 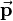$\vec{\mathbf{p}}$. Now a new notation is introduced to represent a transformation using two quaternions $e$ and $p$:

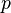$\mathbf{T} = \left[\begin{array}{cccc} & & & \\ & \mathbf{R} & & \vec{\mathbf{p}} \\ & & & \\ 0 & 0 & 0 & 1\end{array}\right] \equiv \left\{e,p\right\}$