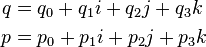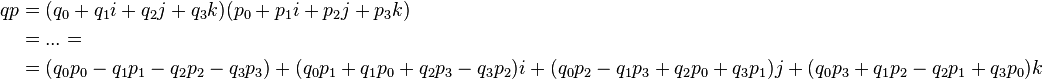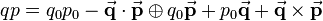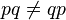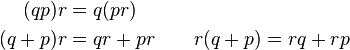Difference between revisions of "Multiplication of quaternions"
| Line 31: | Line 31: | ||
\begin{align} | \begin{align} | ||
(qp)r &= q(pr) \\ | (qp)r &= q(pr) \\ | ||
| − | (q+p)r &= qr+pr \qquad r(q+p) | + | (q+p)r &= qr+pr \qquad r(q+p) = rq+rp |
\end{align} | \end{align} | ||
</math> | </math> | ||
Latest revision as of 15:57, 15 October 2015
| ← Back: Addition of quaternions | Overview: Quaternions | Next: Rotations using quaternions → |
Multiplying two quaternions results in a quaternion again. Assume two quaternions:
Like the addition of two quaternions, the multiplication can as well be solved by just replacing the two quaternions by their equations shown above and then solving the multiplication using regular mathematical rules. Like it is presented in the lecture notes in chapter 3.10.3, this leads to the following:
This expression can be reduced to the following using vector notation:
Expanding this equation leads to the same result like it is presented above (see lecture notes for proof).
The equation above shows, that the multiplication of two quaternions is not commutative because the cross product is not commutative:
Multiplication is only commutative if the two vector parts are linearly dependent which leads to a cross product of zero.
But multiplication of two quaternions is associative and distributive over addition: