Difference between revisions of "Realization of transformations"
From Robotics
| Line 6: | Line 6: | ||
</math> | </math> | ||
The quaternion <math>e</math> is equivalent to <math>\mathbf{R}</math> and describes the rotation while <math>p</math> is defined as <math>0 \oplus \vec{\mathbf{p}}</math> and so equivalent to the translation. | The quaternion <math>e</math> is equivalent to <math>\mathbf{R}</math> and describes the rotation while <math>p</math> is defined as <math>0 \oplus \vec{\mathbf{p}}</math> and so equivalent to the translation. | ||
| + | :<math> | ||
| + | e \equiv \mathbf{R} \qquad \quad p = 0 \oplus \vec{\mathbf{p}} | ||
| + | </math> | ||
Revision as of 10:55, 15 October 2015
| ← Back: Composition of rotations | Overview: Quaternions | Next: ??? → |
Up to now transformations have been defined by homogeneous matrices combining a rotation matrix  and a translation vector
and a translation vector 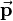 . Now a new notation is introduced to represent a transformation using two quaternions
. Now a new notation is introduced to represent a transformation using two quaternions  and
and 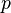 :
:
The quaternion  is equivalent to
is equivalent to  and describes the rotation while
and describes the rotation while 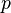 is defined as
is defined as 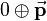 and so equivalent to the translation.
and so equivalent to the translation.
![\mathbf{T} = \left[\begin{array}{cccc} & & & \\ & \mathbf{R} & & \vec{\mathbf{p}} \\ & & & \\ 0 & 0 & 0 & 1\end{array}\right] \equiv \left\{e,p\right\}](/wiki/robotics/images/math/3/0/1/301a5ffd539de858c0981e0180640b3f.png)
