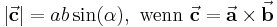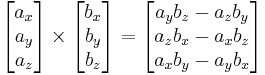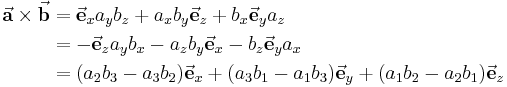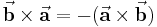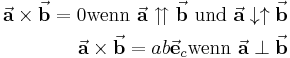Vektorprodukt: Unterschied zwischen den Versionen
| Zeile 29: | Zeile 29: | ||
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
| − | \vec{\textbf{a}}\times\vec{\textbf{b}} | + | \vec{\textbf{a}}\times\vec{\textbf{b}} = 0 \text{wenn}\ \vec{\textbf{a}} \upuparrows \vec{\textbf{b}}\ \text{und}\ \vec{\textbf{a}} \downarrow\uparrow \vec{\textbf{b}}\\ |
| − | \vec{\textbf{a}}\times\vec{\textbf{b}} | + | \vec{\textbf{a}}\times\vec{\textbf{b}} = a b \vec{\textbf{e}}_c \text{wenn}\ \vec{\textbf{a}} \perp \vec{\textbf{b}} |
\end{align} | \end{align} | ||
Version vom 4. Februar 2012, 17:30 Uhr
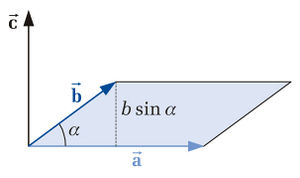
Bei der Multiplikation zweier Vektoren handelt es sich entweder um das Vektorprodukt (auch Kreuzprodukt genannt) oder aber um das Skalarprodukt. Das Skalarprodukt liefert als Ergebnis ein Skalar, das Vektorprodukt hingegen liefert als Ergebnis wieder einen Vektor. Betrachtet man zwei Vektoren 
und 
, so erhält man als Ergebnis des Vektorprodukts einen Vektor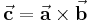 
, der senkrecht auf der von und aufgespannten Fläche steht (siehe Abbildung). Weiterhin bilden die drei Vektoren , und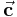 
ein Rechtssystem, das heißt sie sind gemäß der Rechten-Hand-Regel I miteinander verknüpft. Der Betrag des Vektors 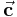lässt sich als Flächeninhalt des von und aufgespannten Parallelogramms interpretieren und wird wie folgt bestimmt:
Dabei bezeichnet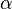 
den Winkel, der von den beiden Vektoren eingeschlossen wird und Werte zwischen 
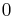und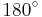 
annehmen kann (siehe Abbildung). Weiterhin gilt es zu beachten, dass das Vektorprodukt ausschließlich für den dreidimensionalen euklidischen Vektorraum definiert ist. Rechnerisch gilt der folgende Zusammenhang:
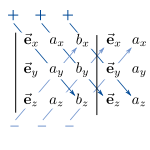
Als Merkhilfe für diesen Zusammenhang eignet sich die Regel von Sarrus: Entsprechend der Abbildung werden dabei die Einheitsvektoren des kartesischen Koordinatensystems in eine erste Spalte und die anderen beiden Vektoren in eine zweite und dritte Spalte geschrieben. Auf diese Weise erhält man eine Matrix, deren ersten beiden Spalten nun erneut rechts neben diese Matrix geschrieben werden. Nun führt man die Multiplikationen und Additionen wie in der Abbildung gezeigt aus und erhält:
Aus mathematischer Sicht bestimmt auf diese Weise die Determinante der genannten Matrix. Anhand der beschriebenen Zusammenhänge zeigt sich, dass das Skalarprodukt nicht dem Kommutativgesetz genügt. Stattdessen gilt:
Weiterhin ergeben sich einige Sonderfälle, die im technischen Kontext häufig zu Vereinfachungen führen:
 Beispiel: Beispiel für das Vektorprodukt
Beispiel. |
