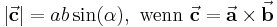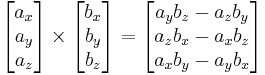Vektorprodukt: Unterschied zwischen den Versionen
| Zeile 7: | Zeile 7: | ||
</math> | </math> | ||
Dabei bezeichnet <math>\alpha</math> den Winkel, der von den beiden Vektoren eingeschlossen wird und Werte zwischen <math>0</math> und <math>180^\circ</math> annehmen kann (siehe Abbildung). Weiterhin gilt es zu beachten, dass das Vektorprodukt ausschließlich für den dreidimensionalen euklidischen Vektorraum definiert ist. Dabei gilt der folgende Zusammenhang: | Dabei bezeichnet <math>\alpha</math> den Winkel, der von den beiden Vektoren eingeschlossen wird und Werte zwischen <math>0</math> und <math>180^\circ</math> annehmen kann (siehe Abbildung). Weiterhin gilt es zu beachten, dass das Vektorprodukt ausschließlich für den dreidimensionalen euklidischen Vektorraum definiert ist. Dabei gilt der folgende Zusammenhang: | ||
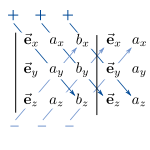
| − | <math> | + | :<math> |
\begin{align} | \begin{align} | ||
\begin{bmatrix} a_x\\ a_y\\ a_z\end{bmatrix} \times \begin{bmatrix} b_x\\ b_y\\ b_z\end{bmatrix} = | \begin{bmatrix} a_x\\ a_y\\ a_z\end{bmatrix} \times \begin{bmatrix} b_x\\ b_y\\ b_z\end{bmatrix} = | ||
Version vom 4. Februar 2012, 15:59 Uhr
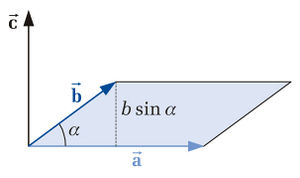
Bei der Multiplikation zweier Vektoren handelt es sich entweder um das Vektorprodukt (auch Kreuzprodukt genannt) oder aber um das Skalarprodukt. Das Skalarprodukt liefert als Ergebnis ein Skalar, das Vektorprodukt hingegen liefert als Ergebnis wieder einen Vektor. Betrachtet man zwei Vektoren 
und 
, so erhält man als Ergebnis des Vektorprodukts einen Vektor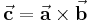 
, der senkrecht auf der von und aufgespannten Fläche steht (siehe Abbildung). Weiterhin bilden die drei Vektoren , und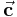 
ein Rechtssystem, das heißt sie sind gemäß der Rechten-Hand-Regel I miteinander verknüpft. Der Betrag des Vektors 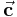lässt sich als Flächeninhalt des von und aufgespannten Parallelogramms interpretieren und wird wie folgt bestimmt:
Dabei bezeichnet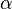 
den Winkel, der von den beiden Vektoren eingeschlossen wird und Werte zwischen 
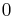und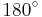 
annehmen kann (siehe Abbildung). Weiterhin gilt es zu beachten, dass das Vektorprodukt ausschließlich für den dreidimensionalen euklidischen Vektorraum definiert ist. Dabei gilt der folgende Zusammenhang:
 Beispiel: Beispiel für das Vektorprodukt
Beispiel. |
