| Um ein Linienintegral bestimmen zu können, etwa um |
Das Linienintegral wird benötigt, wenn eine Funktion von abhängt und entlang einer im Allgemeinen nicht geradlinigen Kontur zu integrieren ist. Dies ist zum Beispiel beim Durchflutungsgesetz der Fall. Prinzipiell handelt es sich um eine Erweiterung der Integralrechnung mit einer und nur einer Integrationsvariablen. Bei einer Integration entlang der x-Achse ist das zugehörige Differential beispielsweise durch 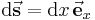 gegeben. Handelt es sich bei dem Integrationsweg C um eine , d. h. der Anfangs- und Endpunkt fallen zusammen (P_A = P_B), wird das Linienintegral als bezeichnet und das Integralzeichen wird mit einem Ring dargestellt. |
| Das Linienintegral wird benötigt, wenn eine Funktion von abhängt und entlang einer im Allgemeinen nicht geradlinigen Kontur zu integrieren ist. Dies ist zum Beispiel beim Durchflutungsgesetz der Fall. Prinzipiell handelt es sich um eine Erweiterung der Integralrechnung mit einer und nur einer Integrationsvariablen. Bei einer Integration entlang der x-Achse ist das zugehörige Differential beispielsweise durch 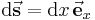gegeben. Handelt es sich bei dem Integrationsweg C um eine , d. h. der Anfangs- und Endpunkt fallen zusammen (P_A = P_B), wird das Linienintegral als bezeichnet und das Integralzeichen wird mit einem Ring dargestellt. |
